Py: Clustering Credit Card Fraud#
This notebook was originally created by Amanda Aitken for the Data Analytics Applications subject, as Case study 2 - Credit card fraud detection in the DAA M06 Unsupervised learning module.
Data Analytics Applications is a Fellowship Applications (Module 3) subject with the Actuaries Institute that aims to teach students how to apply a range of data analytics skills, such as neural networks, natural language processing, unsupervised learning and optimisation techniques, together with their professional judgement, to solve a variety of complex and challenging business problems. The business problems used as examples in this subject are drawn from a wide range of industries.
Find out more about the course here.
Define the problem#
Fraud involves deceptive actions that are taken with the intention of illegally or unethically gaining something at the expense of others. Some examples of fraud include:
stealing another person’s credit card details and using these to purchase goods;
providing false information to an insurance company to obtain an insurance benefit that you are not entitled to; and
using another person’s personal information, without their permission, to commit a crime or to deceive or defraud that other person.
In July 2019, the Centre for Counter Fraud Studies at the University of Portsmouth estimated that fraud costs the global economy £3.89 trillion, with losses from fraud rising by 56% in the past decade. Fraudulent behaviour can occur in any industry, including in many of the industries that actuaries typically work in, such as banking and finance.
Fraud detection is a set of activities that are undertaken to identify fraud. Fraud detection can help to rectify the outcomes of any fraudulent behaviour and/or to prevent fraud from occurring in the future.
Identifying Fraud:#
Some methods that can be used to detect fraud are:
reputation list;
rules engine;
supervised machine learning; and
unsupervised machine learning.
A reputation list, or ‘blacklist’, is a relatively static list of known fraudulent identities. For example, a bank’s ‘blacklist’ might include a list of individuals who have previously been convicted of credit card fraud. A drawback of this method is that it is difficult to keep the reputation list up-to-date and it often requires identities to have been found committing fraudulent behaviour in the past before they can be added to the list.
A rules engine approach to fraud detection involves running a set of rules over an activity. If the activity meets one of the rules, it might be further investigated manually. For example, a retailer might use a rules engine to flag any potentially fraudulent online purchases. They might, for example, flag for further investigation any transactions that are over a certain volume or that are being requested for delivery to a foreign country. While rules engines have the benefit of being easy to understand, they can also be hard to keep up-to-date with recent fraudulent activities.
A supervised learning approach to fraud detection involves training a computer to recognise future fraud by providing it with examples of past fraud. For example, a social media site might have a historical dataset that contains a list of new accounts and their attributes (‘features’) as well as a label to indicate whether each new account was opened by a legitimate customer (‘not fraud’) or by someone pretending to be a legitimate customer (‘fraud’). The classification techniques discussed in Module 5 could be used for this supervised learning approach to fraud detection.
Supervised learning, therefore, approximates a rules engine and might be used to create a rules engine. A drawback of this method is that it requires a large dataset of past examples of fraud which can be very ‘expensive’ to obtain, as the exercise of validating historical instances of fraud can be very time-consuming. In addition, past examples of fraud may not be a good indicator of the types of fraud to which an organisation could be subject in the future. In fact, there should be some anticipation that fraudsters will change their strategies over time when they see that their existing methods of fraud are thwarted or investigated.
Unsupervised learning is described in Video 6.6 as being the cutting-edge solution to fraud detection. As discussed in this module, one branch of unsupervised learning, clustering, involves finding subsets of a population that are like each other and different from other subsets. Clustering can be used in fraud detection in one of two ways:
by identifying outliers that are dissimilar to other observations and do not align closely with any of the clusters found in the dataset—these outliers are potential cases of fraud; or, conversely,
by identifying a cluster of observations, when all other observations appear to be more random and not tightly bunched together—this method is described in Video 6.6.
This notebook explores fraud detection using clustering techniques.
References:#
The datasets that are used in this case study were sourced from the following Kaggle competition: https://www.kaggle.com/c/ieee-fraud-detection.
The aim of the competition was to improve the efficacy of fraudulent transaction identification models.
The data originates from real-world e-commerce transactions and contains two different types of datasets. Note that the meaning of some of the features has been masked by the data provider, so it is not clear what all the features mean.
The first dataset contains the following features for each credit card transaction:
TransactionDT: a measurement of the time since a given reference time (this is referenced on the Kaggle site as being ‘timedelta’ rather than an actual timestamp);
TransactionAMT: the payment amount of the transaction in USD;
ProductCD: the product code for each transaction;
card1 - card6: payment card information, such as card type, card category, issue bank, country, etc.;
addr1: customer’s billing region;
addr2: customer’s billing country;
dist1 - dist 2: distances between, for example,billing address, mailing address, zip code, IP address, phone area, etc.;
P_ and R_ emaildomain: purchaser and recipient email domain;
C1 - C14: counting, such as how many addresses are found to be associated with the payment card, etc. (the actual meaning of these fields was masked in the Kaggle dataset);
D1 - D15: timedeltas, such as days between previous transaction, etc;
M1 - M9: matches, such as whether the name on the card matches the name of the customer etc;
V1 - V339: these fields are described on the Kaggle competition site as ‘Vesta engineered rich features, including ranking, counting, and other entity relations’. For example, one of these features might represent the number of times the payment card associated with a IP and email or address appeared in the transaction list in a 24 hour time range.
The training version of the transactions dataset also contains a ‘TransactionID’ identifier for each transaction and a label ‘isFraud’ to indicate whether the transaction was fraudulent.
The second dataset contains ‘identity’ features for each transaction. These features are described on Kaggle as being ‘network connection information (IP, ISP, Proxy, etc) and digital signature (UA/browser/os/version, etc) associated with transactions’. These features were ‘collected by Vesta’s fraud protection system and digital security partners’. The actual meaning of each of these fields is masked. These features have the following names:
id_01 - id_38;
DeviceType; and
DeviceInfo.
Both the transactions and identity datasets also contain a ‘TransactionID’ column that allows the two datasets to be joined together.
The above information about the features contained in these datasets was sourced from the following Kaggle webpage: https://www.kaggle.com/c/ieee-fraud-detection/discussion/101203.
Packages#
This section installs packages that will be required for this exercise/case study.
# Packages for data management and mathematical operations.
import pandas as pd
import numpy as np
# Package for plotting.
import matplotlib.pyplot as plt
# Scikit-learn libraries to perform clustering and evaluation.
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix, f1_score
# Package used in the confusion matrix function.
import itertools
Functions#
This section defines functions that will be used for this exercise/case study.
# Define a function that helps to format headings in the cell outputs.
def heading(string):
'''
This function is used to print a bold heading followed by a new line.
'''
print('\033[1m'+string+'\033[0m\n')
# The '\033[1m' at the start of the string makes the font bold
# and the '\033[0m' at the end of the string makes the font go back to normal.
# The '\n' at the very end of the string prints a new line to give some space
# before the next item is printed to the output box.
# Define a function to plot confusion matrices in an easy to visualise format.
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
'''
This function prints and plots a nicely formatted confusion matrix.
'''
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment='center',
color='white' if cm[i, j] > thresh else 'black')
plt.tight_layout()
plt.ylabel('True response')
plt.xlabel('Predicted response')
Data#
This section:
imports the data that will be used in the modelling;
explores the data; and
prepares the data for modelling.
Import data#
The code below uploads the following two csv files needed for this case study:
DAA_M06_CS2_data1_transaction.csv (the transaction data); and
DAA_M06_CS2_data2_identity.csv (the identity data).
Note that the transaction dataset is very large (667MB) hence the file is zipped - but pandas is able to read zipped csv files directly.
# Specify the folder that your datasets are saved in.
# or here, read it from the URL
infolder = 'https://actuariesinstitute.github.io/cookbook/_static/daa_datasets/'
# Import the transaction data.
# Specify the filename.
file1 = 'DAA_M06_CS2_data1_transaction.csv.zip'
# Read in the data.
transaction = pd.read_csv (infolder+file1)
# Import the identity data.
# Specify the filename.
file2 = 'DAA_M06_CS2_data2_identity.csv.zip'
# Read in the data.
identity = pd.read_csv (infolder+file2)
Explore data (EDA)#
# Force all columns in the datasets to be shown.
pd.options.display.max_columns = 999
# Print the first 5 rows of each dataset.
heading('Transaction dataset')
print(transaction.head())
print('\n')
heading('Identity dataset')
print(identity.head())
Transaction dataset
TransactionID isFraud TransactionDT TransactionAmt ProductCD card1 \
0 2987000 0 86400 68.5 W 13926
1 2987001 0 86401 29.0 W 2755
2 2987002 0 86469 59.0 W 4663
3 2987003 0 86499 50.0 W 18132
4 2987004 0 86506 50.0 H 4497
card2 card3 card4 card5 card6 addr1 addr2 dist1 dist2 \
0 NaN 150.0 discover 142.0 credit 315.0 87.0 19.0 NaN
1 404.0 150.0 mastercard 102.0 credit 325.0 87.0 NaN NaN
2 490.0 150.0 visa 166.0 debit 330.0 87.0 287.0 NaN
3 567.0 150.0 mastercard 117.0 debit 476.0 87.0 NaN NaN
4 514.0 150.0 mastercard 102.0 credit 420.0 87.0 NaN NaN
P_emaildomain R_emaildomain C1 C2 C3 C4 C5 C6 C7 C8 C9 \
0 NaN NaN 1.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 1.0
1 gmail.com NaN 1.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0
2 outlook.com NaN 1.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 1.0
3 yahoo.com NaN 2.0 5.0 0.0 0.0 0.0 4.0 0.0 0.0 1.0
4 gmail.com NaN 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0
C10 C11 C12 C13 C14 D1 D2 D3 D4 D5 D6 D7 D8 D9 \
0 0.0 2.0 0.0 1.0 1.0 14.0 NaN 13.0 NaN NaN NaN NaN NaN NaN
1 0.0 1.0 0.0 1.0 1.0 0.0 NaN NaN 0.0 NaN NaN NaN NaN NaN
2 0.0 1.0 0.0 1.0 1.0 0.0 NaN NaN 0.0 NaN NaN NaN NaN NaN
3 0.0 1.0 0.0 25.0 1.0 112.0 112.0 0.0 94.0 0.0 NaN NaN NaN NaN
4 1.0 1.0 0.0 1.0 1.0 0.0 NaN NaN NaN NaN NaN NaN NaN NaN
D10 D11 D12 D13 D14 D15 M1 M2 M3 M4 M5 M6 M7 M8 \
0 13.0 13.0 NaN NaN NaN 0.0 T T T M2 F T NaN NaN
1 0.0 NaN NaN NaN NaN 0.0 NaN NaN NaN M0 T T NaN NaN
2 0.0 315.0 NaN NaN NaN 315.0 T T T M0 F F F F
3 84.0 NaN NaN NaN NaN 111.0 NaN NaN NaN M0 T F NaN NaN
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
M9 V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 \
0 NaN 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 0.0 0.0 1.0
2 F 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 1.0 1.0 1.0
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
V15 V16 V17 V18 V19 V20 V21 V22 V23 V24 V25 V26 V27 V28 V29 \
0 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
1 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
2 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
3 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
V30 V31 V32 V33 V34 V35 V36 V37 V38 V39 V40 V41 V42 V43 V44 \
0 0.0 0.0 0.0 0.0 0.0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 0.0 0.0 1.0
2 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 1.0 0.0 0.0 1.0
3 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 1.0 0.0 0.0 1.0
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
V45 V46 V47 V48 V49 V50 V51 V52 V53 V54 V55 V56 V57 V58 V59 \
0 NaN NaN NaN NaN NaN NaN NaN NaN 1.0 1.0 1.0 1.0 0.0 0.0 0.0
1 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0
2 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
3 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
V60 V61 V62 V63 V64 V65 V66 V67 V68 V69 V70 V71 V72 V73 V74 \
0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
3 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
V75 V76 V77 V78 V79 V80 V81 V82 V83 V84 V85 V86 V87 V88 V89 \
0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 0.0
1 0.0 0.0 1.0 1.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0
2 1.0 1.0 1.0 1.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0
3 1.0 1.0 1.0 1.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 0.0
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
V90 V91 V92 V93 V94 V95 V96 V97 V98 V99 V100 V101 V102 \
0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0
1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
3 0.0 0.0 0.0 0.0 0.0 1.0 48.0 28.0 0.0 10.0 4.0 1.0 38.0
4 NaN NaN NaN NaN NaN 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V103 V104 V105 V106 V107 V108 V109 V110 V111 V112 V113 V114 \
0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
2 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
3 24.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
4 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
V115 V116 V117 V118 V119 V120 V121 V122 V123 V124 V125 V126 \
0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0
1 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0
2 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0
3 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 50.0
4 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0
V127 V128 V129 V130 V131 V132 V133 V134 V135 V136 V137 \
0 117.0 0.0 0.0 0.0 0.0 0.0 117.0 0.0 0.0 0.0 0.0
1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
3 1758.0 925.0 0.0 354.0 135.0 50.0 1404.0 790.0 0.0 0.0 0.0
4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V138 V139 V140 V141 V142 V143 V144 V145 V146 V147 V148 V149 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 0.0 0.0 0.0 0.0 0.0 6.0 18.0 140.0 0.0 0.0 0.0 0.0
V150 V151 V152 V153 V154 V155 V156 V157 V158 V159 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 1803.0 49.0 64.0 0.0 0.0 0.0 0.0 0.0 0.0 15557.990234
V160 V161 V162 V163 V164 V165 V166 V167 V168 V169 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 169690.796875 0.0 0.0 0.0 515.0 5155.0 2840.0 0.0 0.0 0.0
V170 V171 V172 V173 V174 V175 V176 V177 V178 V179 V180 V181 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 1.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0
V182 V183 V184 V185 V186 V187 V188 V189 V190 V191 V192 V193 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
V194 V195 V196 V197 V198 V199 V200 V201 V202 V203 V204 V205 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0
V206 V207 V208 V209 V210 V211 V212 V213 V214 V215 V216 V217 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V218 V219 V220 V221 V222 V223 V224 V225 V226 V227 V228 V229 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0
V230 V231 V232 V233 V234 V235 V236 V237 V238 V239 V240 V241 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0
V242 V243 V244 V245 V246 V247 V248 V249 V250 V251 V252 V253 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
V254 V255 V256 V257 V258 V259 V260 V261 V262 V263 V264 V265 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0
V266 V267 V268 V269 V270 V271 V272 V273 V274 V275 V276 V277 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V278 V279 V280 V281 V282 V283 V284 V285 V286 V287 V288 V289 \
0 NaN 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0
1 NaN 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0
2 NaN 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0
3 NaN 1.0 28.0 0.0 0.0 0.0 0.0 10.0 0.0 4.0 0.0 0.0
4 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0
V290 V291 V292 V293 V294 V295 V296 V297 V298 V299 V300 V301 \
0 1.0 1.0 1.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
3 1.0 1.0 1.0 1.0 38.0 24.0 0.0 0.0 0.0 0.0 0.0 0.0
4 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V302 V303 V304 V305 V306 V307 V308 V309 V310 V311 V312 \
0 0.0 0.0 0.0 1.0 0.0 117.0 0.0 0.0 0.0 0.0 0.0
1 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
3 0.0 0.0 0.0 1.0 50.0 1758.0 925.0 0.0 354.0 0.0 135.0
4 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V313 V314 V315 V316 V317 V318 V319 V320 V321 V322 V323 V324 \
0 0.0 0.0 0.0 0.0 117.0 0.0 0.0 0.0 0.0 NaN NaN NaN
1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 NaN NaN NaN
2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 NaN NaN NaN
3 0.0 0.0 0.0 50.0 1404.0 790.0 0.0 0.0 0.0 NaN NaN NaN
4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V325 V326 V327 V328 V329 V330 V331 V332 V333 V334 V335 V336 \
0 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
V337 V338 V339
0 NaN NaN NaN
1 NaN NaN NaN
2 NaN NaN NaN
3 NaN NaN NaN
4 0.0 0.0 0.0
Identity dataset
TransactionID id_01 id_02 id_03 id_04 id_05 id_06 id_07 id_08 \
0 2987004 0.0 70787.0 NaN NaN NaN NaN NaN NaN
1 2987008 -5.0 98945.0 NaN NaN 0.0 -5.0 NaN NaN
2 2987010 -5.0 191631.0 0.0 0.0 0.0 0.0 NaN NaN
3 2987011 -5.0 221832.0 NaN NaN 0.0 -6.0 NaN NaN
4 2987016 0.0 7460.0 0.0 0.0 1.0 0.0 NaN NaN
id_09 id_10 id_11 id_12 id_13 id_14 id_15 id_16 id_17 id_18 \
0 NaN NaN 100.0 NotFound NaN -480.0 New NotFound 166.0 NaN
1 NaN NaN 100.0 NotFound 49.0 -300.0 New NotFound 166.0 NaN
2 0.0 0.0 100.0 NotFound 52.0 NaN Found Found 121.0 NaN
3 NaN NaN 100.0 NotFound 52.0 NaN New NotFound 225.0 NaN
4 0.0 0.0 100.0 NotFound NaN -300.0 Found Found 166.0 15.0
id_19 id_20 id_21 id_22 id_23 id_24 id_25 id_26 id_27 id_28 \
0 542.0 144.0 NaN NaN NaN NaN NaN NaN NaN New
1 621.0 500.0 NaN NaN NaN NaN NaN NaN NaN New
2 410.0 142.0 NaN NaN NaN NaN NaN NaN NaN Found
3 176.0 507.0 NaN NaN NaN NaN NaN NaN NaN New
4 529.0 575.0 NaN NaN NaN NaN NaN NaN NaN Found
id_29 id_30 id_31 id_32 id_33 \
0 NotFound Android 7.0 samsung browser 6.2 32.0 2220x1080
1 NotFound iOS 11.1.2 mobile safari 11.0 32.0 1334x750
2 Found NaN chrome 62.0 NaN NaN
3 NotFound NaN chrome 62.0 NaN NaN
4 Found Mac OS X 10_11_6 chrome 62.0 24.0 1280x800
id_34 id_35 id_36 id_37 id_38 DeviceType \
0 match_status:2 T F T T mobile
1 match_status:1 T F F T mobile
2 NaN F F T T desktop
3 NaN F F T T desktop
4 match_status:2 T F T T desktop
DeviceInfo
0 SAMSUNG SM-G892A Build/NRD90M
1 iOS Device
2 Windows
3 NaN
4 MacOS
The outputs above show that there are many features in these two datasets that have missing values (NaN).
# Check the number of observations and features of the data sets.
heading('Transaction dataset')
print(transaction.info())
print('\n')
heading('Identity dataset')
print(identity.info())
Transaction dataset
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 590540 entries, 0 to 590539
Columns: 394 entries, TransactionID to V339
dtypes: float64(376), int64(4), object(14)
memory usage: 1.7+ GB
None
Identity dataset
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 144233 entries, 0 to 144232
Data columns (total 41 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 TransactionID 144233 non-null int64
1 id_01 144233 non-null float64
2 id_02 140872 non-null float64
3 id_03 66324 non-null float64
4 id_04 66324 non-null float64
5 id_05 136865 non-null float64
6 id_06 136865 non-null float64
7 id_07 5155 non-null float64
8 id_08 5155 non-null float64
9 id_09 74926 non-null float64
10 id_10 74926 non-null float64
11 id_11 140978 non-null float64
12 id_12 144233 non-null object
13 id_13 127320 non-null float64
14 id_14 80044 non-null float64
15 id_15 140985 non-null object
16 id_16 129340 non-null object
17 id_17 139369 non-null float64
18 id_18 45113 non-null float64
19 id_19 139318 non-null float64
20 id_20 139261 non-null float64
21 id_21 5159 non-null float64
22 id_22 5169 non-null float64
23 id_23 5169 non-null object
24 id_24 4747 non-null float64
25 id_25 5132 non-null float64
26 id_26 5163 non-null float64
27 id_27 5169 non-null object
28 id_28 140978 non-null object
29 id_29 140978 non-null object
30 id_30 77565 non-null object
31 id_31 140282 non-null object
32 id_32 77586 non-null float64
33 id_33 73289 non-null object
34 id_34 77805 non-null object
35 id_35 140985 non-null object
36 id_36 140985 non-null object
37 id_37 140985 non-null object
38 id_38 140985 non-null object
39 DeviceType 140810 non-null object
40 DeviceInfo 118666 non-null object
dtypes: float64(23), int64(1), object(17)
memory usage: 45.1+ MB
None
# Summarise key information about numeric features in each of the datasets.
heading('Transaction dataset')
print(transaction.describe())
print('\n')
heading('Identity dataset')
print(identity.describe())
Transaction dataset
TransactionID isFraud TransactionDT TransactionAmt \
count 5.905400e+05 590540.000000 5.905400e+05 590540.000000
mean 3.282270e+06 0.034990 7.372311e+06 135.027176
std 1.704744e+05 0.183755 4.617224e+06 239.162522
min 2.987000e+06 0.000000 8.640000e+04 0.251000
25% 3.134635e+06 0.000000 3.027058e+06 43.321000
50% 3.282270e+06 0.000000 7.306528e+06 68.769000
75% 3.429904e+06 0.000000 1.124662e+07 125.000000
max 3.577539e+06 1.000000 1.581113e+07 31937.391000
card1 card2 card3 card5 \
count 590540.000000 581607.000000 588975.000000 586281.000000
mean 9898.734658 362.555488 153.194925 199.278897
std 4901.170153 157.793246 11.336444 41.244453
min 1000.000000 100.000000 100.000000 100.000000
25% 6019.000000 214.000000 150.000000 166.000000
50% 9678.000000 361.000000 150.000000 226.000000
75% 14184.000000 512.000000 150.000000 226.000000
max 18396.000000 600.000000 231.000000 237.000000
addr1 addr2 dist1 dist2 \
count 524834.000000 524834.000000 238269.000000 37627.000000
mean 290.733794 86.800630 118.502180 231.855423
std 101.741072 2.690623 371.872026 529.053494
min 100.000000 10.000000 0.000000 0.000000
25% 204.000000 87.000000 3.000000 7.000000
50% 299.000000 87.000000 8.000000 37.000000
75% 330.000000 87.000000 24.000000 206.000000
max 540.000000 102.000000 10286.000000 11623.000000
C1 C2 C3 C4 \
count 590540.000000 590540.000000 590540.000000 590540.000000
mean 14.092458 15.269734 0.005644 4.092185
std 133.569018 154.668899 0.150536 68.848459
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 0.000000 0.000000
50% 1.000000 1.000000 0.000000 0.000000
75% 3.000000 3.000000 0.000000 0.000000
max 4685.000000 5691.000000 26.000000 2253.000000
C5 C6 C7 C8 \
count 590540.000000 590540.000000 590540.000000 590540.000000
mean 5.571526 9.071082 2.848478 5.144574
std 25.786976 71.508467 61.727304 95.378574
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 1.000000 0.000000 0.000000
50% 0.000000 1.000000 0.000000 0.000000
75% 1.000000 2.000000 0.000000 0.000000
max 349.000000 2253.000000 2255.000000 3331.000000
C9 C10 C11 C12 \
count 590540.000000 590540.000000 590540.000000 590540.000000
mean 4.480240 5.240343 10.241521 4.076227
std 16.674897 95.581443 94.336292 86.666218
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 1.000000 0.000000
50% 1.000000 0.000000 1.000000 0.000000
75% 2.000000 0.000000 2.000000 0.000000
max 210.000000 3257.000000 3188.000000 3188.000000
C13 C14 D1 D2 \
count 590540.000000 590540.000000 589271.000000 309743.000000
mean 32.539918 8.295215 94.347568 169.563231
std 129.364844 49.544262 157.660387 177.315865
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 0.000000 26.000000
50% 3.000000 1.000000 3.000000 97.000000
75% 12.000000 2.000000 122.000000 276.000000
max 2918.000000 1429.000000 640.000000 640.000000
D3 D4 D5 D6 \
count 327662.000000 421618.000000 280699.000000 73187.000000
mean 28.343348 140.002441 42.335965 69.805717
std 62.384721 191.096774 89.000144 143.669253
min 0.000000 -122.000000 0.000000 -83.000000
25% 1.000000 0.000000 1.000000 0.000000
50% 8.000000 26.000000 10.000000 0.000000
75% 27.000000 253.000000 32.000000 40.000000
max 819.000000 869.000000 819.000000 873.000000
D7 D8 D9 D10 D11 \
count 38917.000000 74926.000000 74926.000000 514518.000000 311253.000000
mean 41.638950 146.058108 0.561057 123.982137 146.621465
std 99.743264 231.663840 0.316880 182.615225 186.042622
min 0.000000 0.000000 0.000000 0.000000 -53.000000
25% 0.000000 0.958333 0.208333 0.000000 0.000000
50% 0.000000 37.875000 0.666666 15.000000 43.000000
75% 17.000000 187.958328 0.833333 197.000000 274.000000
max 843.000000 1707.791626 0.958333 876.000000 670.000000
D12 D13 D14 D15 V1 \
count 64717.000000 61952.000000 62187.000000 501427.000000 311253.000000
mean 54.037533 17.901295 57.724444 163.744579 0.999945
std 124.274558 67.614425 136.312450 202.726660 0.007390
min -83.000000 0.000000 -193.000000 -83.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 1.000000
50% 0.000000 0.000000 0.000000 52.000000 1.000000
75% 13.000000 0.000000 2.000000 314.000000 1.000000
max 648.000000 847.000000 878.000000 879.000000 1.000000
V2 V3 V4 V5 \
count 311253.000000 311253.000000 311253.000000 311253.000000
mean 1.045204 1.078075 0.846456 0.876991
std 0.240133 0.320890 0.440053 0.475902
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 8.000000 9.000000 6.000000 6.000000
V6 V7 V8 V9 \
count 311253.000000 311253.000000 311253.000000 311253.000000
mean 1.045686 1.072870 1.027704 1.041529
std 0.239385 0.304779 0.186069 0.226339
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 9.000000 9.000000 8.000000 8.000000
V10 V11 V12 V13 \
count 311253.000000 311253.000000 514467.000000 514467.000000
mean 0.463915 0.478987 0.559711 0.599166
std 0.521522 0.552431 0.510533 0.532185
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 4.000000 5.000000 3.000000 6.000000
V14 V15 V16 V17 \
count 514467.000000 514467.000000 514467.000000 514467.000000
mean 0.999500 0.122342 0.123460 0.134040
std 0.022345 0.332422 0.342841 0.364456
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 0.000000 0.000000 0.000000
50% 1.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000
max 1.000000 7.000000 15.000000 15.000000
V18 V19 V20 V21 \
count 514467.000000 514467.000000 514467.000000 514467.000000
mean 0.135363 0.816371 0.847843 0.129684
std 0.371763 0.425512 0.459451 0.339060
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 1.000000 1.000000 0.000000
50% 0.000000 1.000000 1.000000 0.000000
75% 0.000000 1.000000 1.000000 0.000000
max 15.000000 7.000000 15.000000 5.000000
V22 V23 V24 V25 \
count 514467.000000 514467.000000 514467.000000 514467.000000
mean 0.132292 1.034791 1.058097 0.977660
std 0.359415 0.247681 0.305485 0.185245
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 1.000000 1.000000 1.000000
50% 0.000000 1.000000 1.000000 1.000000
75% 0.000000 1.000000 1.000000 1.000000
max 8.000000 13.000000 13.000000 7.000000
V26 V27 V28 V29 \
count 514467.000000 514467.000000 514467.000000 514467.000000
mean 0.988040 0.000776 0.000830 0.387840
std 0.209302 0.028596 0.031133 0.510652
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 0.000000 0.000000 0.000000
50% 1.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 1.000000
max 13.000000 4.000000 4.000000 5.000000
V30 V31 V32 V33 \
count 514467.000000 514467.000000 514467.000000 514467.000000
mean 0.406436 0.140761 0.142417 0.130693
std 0.554311 0.355793 0.368278 0.340900
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000
max 9.000000 7.000000 15.000000 7.000000
V34 V35 V36 V37 \
count 514467.000000 421571.000000 421571.000000 421571.000000
mean 0.139154 0.542594 0.579198 1.108065
std 0.357549 0.516010 0.539039 0.690571
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 1.000000
50% 0.000000 1.000000 1.000000 1.000000
75% 0.000000 1.000000 1.000000 1.000000
max 13.000000 3.000000 5.000000 54.000000
V38 V39 V40 V41 \
count 421571.00000 421571.000000 421571.000000 421571.000000
mean 1.16240 0.166076 0.177145 0.999269
std 0.85892 0.451956 0.505786 0.027020
min 0.00000 0.000000 0.000000 0.000000
25% 1.00000 0.000000 0.000000 1.000000
50% 1.00000 0.000000 0.000000 1.000000
75% 1.00000 0.000000 0.000000 1.000000
max 54.00000 15.000000 24.000000 1.000000
V42 V43 V44 V45 \
count 421571.000000 421571.000000 421571.000000 421571.000000
mean 0.156118 0.168942 1.083891 1.120779
std 0.382896 0.433359 0.639143 0.729774
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 1.000000 1.000000
50% 0.000000 0.000000 1.000000 1.000000
75% 0.000000 0.000000 1.000000 1.000000
max 8.000000 8.000000 48.000000 48.000000
V46 V47 V48 V49 \
count 421571.000000 421571.000000 421571.000000 421571.000000
mean 1.022286 1.038515 0.383174 0.397724
std 0.166719 0.231862 0.508189 0.542654
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 0.000000 0.000000
50% 1.000000 1.000000 0.000000 0.000000
75% 1.000000 1.000000 1.000000 1.000000
max 6.000000 12.000000 5.000000 5.000000
V50 V51 V52 V53 \
count 421571.000000 421571.000000 421571.000000 513444.000000
mean 0.164746 0.170579 0.182695 0.577586
std 0.373995 0.403899 0.439002 0.511571
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 1.000000
75% 0.000000 0.000000 0.000000 1.000000
max 5.000000 6.000000 12.000000 5.000000
V54 V55 V56 V57 \
count 513444.000000 513444.000000 513444.000000 513444.000000
mean 0.619982 1.067670 1.120979 0.128312
std 0.534635 0.391364 0.661129 0.349094
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 1.000000 1.000000 0.000000
50% 1.000000 1.000000 1.000000 0.000000
75% 1.000000 1.000000 1.000000 0.000000
max 6.000000 17.000000 51.000000 6.000000
V58 V59 V60 V61 \
count 513444.000000 513444.000000 513444.000000 513444.000000
mean 0.132453 0.134433 0.142537 0.829785
std 0.372907 0.379291 0.418230 0.436617
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 1.000000
50% 0.000000 0.000000 0.000000 1.000000
75% 0.000000 0.000000 0.000000 1.000000
max 10.000000 16.000000 16.000000 6.000000
V62 V63 V64 V65 \
count 513444.000000 513444.000000 513444.000000 513444.000000
mean 0.867563 0.130743 0.141825 0.999663
std 0.483803 0.355262 0.406157 0.018353
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 0.000000 0.000000 1.000000
50% 1.000000 0.000000 0.000000 1.000000
75% 1.000000 0.000000 0.000000 1.000000
max 10.000000 7.000000 7.000000 1.000000
V66 V67 V68 V69 \
count 513444.000000 513444.000000 513444.000000 513444.000000
mean 0.981038 0.998121 0.000534 0.390200
std 0.216235 0.245912 0.023760 0.513696
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 0.000000 0.000000
50% 1.000000 1.000000 0.000000 0.000000
75% 1.000000 1.000000 0.000000 1.000000
max 7.000000 8.000000 2.000000 5.000000
V70 V71 V72 V73 \
count 513444.000000 513444.000000 513444.000000 513444.000000
mean 0.407924 0.140639 0.145124 0.139982
std 0.554499 0.364303 0.389212 0.367098
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000
max 6.000000 6.000000 10.000000 7.000000
V74 V75 V76 V77 \
count 513444.000000 501376.000000 501376.000000 501376.000000
mean 0.152147 0.544278 0.587557 1.086893
std 0.393274 0.514318 0.538230 0.532958
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 1.000000
50% 0.000000 1.000000 1.000000 1.000000
75% 0.000000 1.000000 1.000000 1.000000
max 8.000000 4.000000 6.000000 30.000000
V78 V79 V80 V81 \
count 501376.000000 501376.000000 501376.000000 501376.000000
mean 1.144462 0.136867 0.143954 0.152696
std 0.781474 0.379904 0.409932 0.452298
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 0.000000 0.000000 0.000000
50% 1.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000
max 31.000000 7.000000 19.000000 19.000000
V82 V83 V84 V85 \
count 501376.000000 501376.000000 501376.000000 501376.000000
mean 0.844610 0.881965 0.137145 0.149788
std 0.422529 0.470757 0.361875 0.419445
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 0.000000 0.000000
50% 1.000000 1.000000 0.000000 0.000000
75% 1.000000 1.000000 0.000000 0.000000
max 7.000000 7.000000 7.000000 7.000000
V86 V87 V88 V89 \
count 501376.000000 501376.000000 501376.000000 501376.000000
mean 1.064885 1.099456 0.999246 0.000902
std 0.419807 0.511281 0.027447 0.031943
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 0.000000
50% 1.000000 1.000000 1.000000 0.000000
75% 1.000000 1.000000 1.000000 0.000000
max 30.000000 30.000000 1.000000 2.000000
V90 V91 V92 V93 \
count 501376.000000 501376.000000 501376.000000 501376.000000
mean 0.401862 0.420461 0.150322 0.154812
std 0.516153 0.561865 0.375682 0.402314
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 1.000000 1.000000 0.000000 0.000000
max 5.000000 6.000000 7.000000 7.000000
V94 V95 V96 V97 \
count 501376.000000 590226.000000 590226.00000 590226.000000
mean 0.137007 1.038019 3.00519 1.718933
std 0.343878 21.034304 40.23949 27.700449
min 0.000000 0.000000 0.00000 0.000000
25% 0.000000 0.000000 0.00000 0.000000
50% 0.000000 0.000000 0.00000 0.000000
75% 0.000000 0.000000 1.00000 0.000000
max 2.000000 880.000000 1410.00000 976.000000
V98 V99 V100 V101 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 0.061985 0.894986 0.273504 0.889249
std 0.284995 2.722552 0.947176 20.582571
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 1.000000 0.000000 0.000000
max 12.000000 88.000000 28.000000 869.000000
V102 V103 V104 V105 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 1.827229 1.279288 0.085433 0.281145
std 35.928456 25.685642 0.648718 3.373948
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 1285.000000 928.000000 15.000000 99.000000
V106 V107 V108 V109 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 0.164584 0.999580 1.004613 1.014816
std 1.825665 0.020494 0.081146 0.127769
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 1.000000 1.000000 1.000000
50% 0.000000 1.000000 1.000000 1.000000
75% 0.000000 1.000000 1.000000 1.000000
max 55.000000 1.000000 7.000000 7.000000
V110 V111 V112 V113 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 1.007739 1.002563 1.005356 1.003383
std 0.097290 0.070830 0.084617 0.074754
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 7.000000 9.000000 9.000000 9.000000
V114 V115 V116 V117 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 1.009298 1.032450 1.015738 1.000391
std 0.110179 0.190385 0.136770 0.035238
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 6.000000 6.000000 6.000000 3.000000
V118 V119 V120 V121 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 1.001474 1.000729 1.000874 1.004276
std 0.041011 0.036392 0.041684 0.067097
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 3.000000 3.000000 3.000000 3.000000
V122 V123 V124 V125 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 1.001759 1.031120 1.092975 1.050415
std 0.048636 0.228134 0.374103 0.280037
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 3.000000 13.000000 13.000000 13.000000
V126 V127 V128 V129 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 129.979417 336.611559 204.094038 8.768944
std 2346.951681 4238.666949 3010.258774 113.832828
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 107.949997 0.000000 0.000000
max 160000.000000 160000.000000 160000.000000 55125.000000
V130 V131 V132 V133 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 92.165849 31.133302 103.513188 204.889160
std 315.960485 161.161258 2266.106140 3796.316755
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 59.000000 0.000000 0.000000 0.000000
max 55125.000000 55125.000000 93736.000000 133915.000000
V134 V135 V136 V137 \
count 590226.000000 590226.000000 590226.000000 590226.000000
mean 145.972328 17.250132 38.821196 26.365090
std 2772.986817 293.847563 451.808411 348.332714
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 98476.000000 90750.000000 90750.000000 90750.000000
V138 V139 V140 V141 V142 \
count 81945.000000 81945.000000 81945.000000 81945.000000 81945.000000
mean 0.036439 1.073915 1.125267 0.037696 0.048581
std 0.428490 1.333924 1.467850 0.215133 0.313888
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 0.000000 1.000000 1.000000 0.000000 0.000000
75% 0.000000 1.000000 1.000000 0.000000 0.000000
max 22.000000 33.000000 33.000000 5.000000 9.000000
V143 V144 V145 V146 V147 \
count 81951.000000 81951.000000 81951.000000 81945.000000 81945.000000
mean 8.397006 3.708484 22.112946 0.156276 0.168601
std 55.267545 10.485633 64.371860 0.682328 0.750497
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 1.000000 0.000000 0.000000
max 869.000000 62.000000 297.000000 24.000000 26.000000
V148 V149 V150 V151 V152 \
count 81945.000000 81945.000000 81951.000000 81951.000000 81951.000000
mean 0.765001 0.775313 277.598028 6.460190 9.432710
std 0.581425 0.628191 829.576922 15.232324 21.554486
min 0.000000 0.000000 1.000000 1.000000 1.000000
25% 0.000000 0.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000 1.000000
max 20.000000 20.000000 3389.000000 57.000000 69.000000
V153 V154 V155 V156 V157 \
count 81945.000000 81945.000000 81945.000000 81945.000000 81945.000000
mean 0.753200 0.757423 0.767381 0.777485 0.817573
std 0.532649 0.546907 0.602678 0.647209 0.682016
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 1.000000 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000 1.000000
max 18.000000 18.000000 24.000000 24.000000 24.000000
V158 V159 V160 V161 V162 \
count 81945.000000 81951.000000 81951.000000 81945.000000 81945.000000
mean 0.833461 2719.299775 47453.181173 4.843938 6.594661
std 0.734336 8355.445049 142076.069162 58.929757 69.195180
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 1.000000 0.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000 0.000000
max 24.000000 55125.000000 641511.437500 3300.000000 3300.000000
V163 V164 V165 V166 V167 \
count 81945.000000 81951.000000 81951.000000 81951.000000 139631.000000
mean 5.505955 877.888928 2239.912219 359.469437 3.929514
std 63.077887 6049.166505 8223.258928 1244.463270 42.200980
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000 0.000000
max 3300.000000 93736.000000 98476.000000 104060.000000 872.000000
V168 V169 V170 V171 \
count 139631.000000 139819.000000 139819.000000 139819.000000
mean 5.859501 0.168053 1.436779 1.690908
std 54.032468 0.904944 1.751143 2.444748
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 1.000000 1.000000
50% 0.000000 0.000000 1.000000 1.000000
75% 1.000000 0.000000 1.000000 1.000000
max 964.000000 19.000000 48.000000 61.000000
V172 V173 V174 V175 \
count 139631.000000 139631.000000 139819.000000 139819.000000
mean 0.132012 0.055231 0.127794 0.212639
std 0.924894 0.264439 0.379763 0.857133
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 31.000000 7.000000 8.000000 14.000000
V176 V177 V178 V179 \
count 139631.000000 139631.000000 139631.000000 139631.000000
mean 1.376979 3.529245 6.649283 4.869012
std 1.829420 41.310622 69.447364 50.489426
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 0.000000 0.000000 0.000000
50% 1.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000
max 48.000000 861.000000 1235.000000 920.000000
V180 V181 V182 V183 \
count 139819.000000 139631.000000 139631.000000 139631.000000
mean 0.924123 0.253332 0.856243 0.484692
std 6.112630 1.248974 5.792934 2.946982
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 83.000000 24.000000 83.000000 41.000000
V184 V185 V186 V187 \
count 139819.000000 139819.000000 139631.000000 139631.000000
mean 0.132364 0.173903 1.148799 1.843752
std 0.543699 0.699733 1.223529 9.884390
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 1.000000 1.000000
50% 0.000000 0.000000 1.000000 1.000000
75% 0.000000 0.000000 1.000000 1.000000
max 16.000000 31.000000 38.000000 218.000000
V188 V189 V190 V191 \
count 139819.000000 139819.000000 139631.000000 139631.000000
mean 1.014755 1.038314 1.213083 1.058984
std 0.671207 0.792528 1.480318 0.677527
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 30.000000 30.000000 42.000000 21.000000
V192 V193 V194 V195 \
count 139631.000000 139631.000000 139819.000000 139819.000000
mean 1.237361 1.149845 0.945773 0.954227
std 2.635961 1.714792 0.304158 0.376420
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 44.000000 37.000000 7.000000 16.000000
V196 V197 V198 V199 \
count 139631.000000 139819.000000 139819.000000 139631.000000
mean 1.084580 0.949385 0.961951 1.270749
std 1.105834 0.336871 0.493065 1.671863
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 38.000000 14.000000 21.000000 45.000000
V200 V201 V202 V203 \
count 139819.000000 139819.000000 139631.000000 139631.000000
mean 1.119977 1.159106 444.147142 1078.327538
std 1.253853 1.418618 4683.828419 9105.607991
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 0.000000 0.000000
50% 1.000000 1.000000 0.000000 0.000000
75% 1.000000 1.000000 0.000000 30.924400
max 45.000000 55.000000 104060.000000 139777.000000
V204 V205 V206 V207 \
count 139631.000000 139631.000000 139631.000000 139631.000000
mean 686.956931 18.060417 6.189360 72.284098
std 6048.980716 266.545451 191.474014 925.676660
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 20.000000 0.000000 0.000000 0.000000
max 104060.000000 55125.000000 55125.000000 55125.000000
V208 V209 V210 V211 \
count 139819.000000 139819.000000 139819.000000 139631.000000
mean 8.888193 35.001872 14.391835 385.137037
std 59.047125 250.800822 86.523724 4541.837915
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 3300.000000 8050.000000 3300.000000 92888.000000
V212 V213 V214 V215 \
count 139631.000000 139631.000000 139631.000000 139631.000000
mean 765.988339 536.302802 38.437547 133.208217
std 7496.120737 5471.664736 571.834283 1040.453748
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 129006.000000 97628.000000 104060.000000 104060.000000
V216 V217 V218 V219 \
count 139631.000000 130430.000000 130430.000000 130430.000000
mean 71.107143 1.054619 1.725784 1.367132
std 680.267625 9.547354 13.919876 12.044032
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 1.000000 1.000000
max 104060.000000 303.000000 400.000000 378.000000
V220 V221 V222 V223 \
count 141416.000000 141416.000000 141416.000000 130430.000000
mean 0.169472 1.274912 1.359005 0.093153
std 1.002463 2.728792 2.913772 0.402232
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 1.000000 1.000000 0.000000
50% 0.000000 1.000000 1.000000 0.000000
75% 0.000000 1.000000 1.000000 0.000000
max 25.000000 384.000000 384.000000 16.000000
V224 V225 V226 V227 \
count 130430.000000 130430.000000 130430.000000 141416.000000
mean 0.394748 0.191758 0.247612 0.147975
std 3.443310 1.290820 2.756449 2.049363
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 144.000000 51.000000 242.000000 360.000000
V228 V229 V230 V231 \
count 130430.000000 130430.000000 130430.000000 130430.000000
mean 1.351928 1.638710 1.465476 0.765506
std 1.409722 4.316026 2.122783 8.877119
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 0.000000
50% 1.000000 1.000000 1.000000 0.000000
75% 1.000000 1.000000 1.000000 0.000000
max 54.000000 176.000000 65.000000 293.000000
V232 V233 V234 V235 \
count 130430.000000 130430.000000 141416.000000 130430.000000
mean 1.005597 0.908388 2.092847 0.184106
std 10.460253 10.149884 11.323036 0.902639
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 337.000000 332.000000 121.000000 23.000000
V236 V237 V238 V239 \
count 130430.000000 130430.000000 141416.000000 141416.000000
mean 0.307667 0.253500 0.127956 0.136965
std 2.152332 1.716634 0.574657 0.616260
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 45.000000 39.000000 23.000000 23.000000
V240 V241 V242 V243 \
count 130430.000000 130430.000000 130430.000000 130430.000000
mean 1.000997 1.000238 1.113463 1.178387
std 0.049522 0.022663 0.660110 1.398953
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 7.000000 5.000000 20.000000 57.000000
V244 V245 V246 V247 \
count 130430.000000 141416.000000 130430.000000 130430.000000
mean 1.118562 0.876619 1.183723 1.025355
std 0.698807 1.821065 1.040363 0.281604
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 22.000000 262.000000 45.000000 18.000000
V248 V249 V250 V251 \
count 130430.000000 130430.000000 141416.000000 141416.000000
mean 1.069493 1.042851 0.788588 0.794231
std 0.888341 0.528812 0.488386 0.501240
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 36.000000 22.000000 18.000000 18.000000
V252 V253 V254 V255 \
count 130430.000000 130430.000000 130430.000000 141416.000000
mean 1.032048 1.162164 1.075113 0.806656
std 0.389546 3.612553 1.357550 0.939124
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 24.000000 163.000000 60.000000 87.000000
V256 V257 V258 V259 \
count 141416.000000 130430.000000 130430.000000 141416.000000
mean 0.814950 1.250993 1.343510 0.967832
std 0.969953 1.299956 2.015811 2.113447
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 1.000000
50% 1.000000 1.000000 1.000000 1.000000
75% 1.000000 1.000000 1.000000 1.000000
max 87.000000 48.000000 66.000000 285.000000
V260 V261 V262 V263 \
count 130430.000000 130430.000000 130430.000000 130430.000000
mean 0.964425 1.107161 1.013279 117.390676
std 0.379828 1.323230 0.625455 1294.851543
min 0.000000 0.000000 0.000000 0.000000
25% 1.000000 1.000000 1.000000 0.000000
50% 1.000000 1.000000 1.000000 0.000000
75% 1.000000 1.000000 1.000000 0.000000
max 8.000000 49.000000 20.000000 153600.000000
V264 V265 V266 V267 \
count 130430.000000 130430.000000 130430.000000 130430.000000
mean 201.657617 153.520534 9.167839 36.525103
std 2284.827492 1605.512276 208.038863 644.878586
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 33.593498 20.897525 0.000000 0.000000
max 153600.000000 153600.000000 55125.000000 55125.000000
V268 V269 V270 V271 \
count 130430.000000 130430.000000 141416.000000 141416.000000
mean 18.813407 5.997508 7.712764 9.445133
std 311.280181 207.317539 65.507232 74.147726
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 55125.000000 55125.000000 4000.000000 4000.000000
V272 V273 V274 V275 \
count 141416.000000 130430.000000 130430.000000 130430.000000
mean 8.464571 73.825549 107.151636 88.899939
std 69.723735 935.187927 1258.734139 1072.883139
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 4000.000000 51200.000000 66000.000000 51200.000000
V276 V277 V278 V279 \
count 130430.000000 130430.000000 130430.000000 590528.000000
mean 31.797277 51.956645 42.328228 1.123061
std 615.659714 732.145368 660.611820 21.021950
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 104060.000000 104060.000000 104060.000000 880.000000
V280 V281 V282 V283 \
count 590528.000000 589271.000000 589271.000000 589271.000000
mean 1.967082 0.087783 0.817171 0.991114
std 27.851780 0.512748 0.921880 1.558731
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 1.000000 1.000000
75% 1.000000 0.000000 1.000000 1.000000
max 975.000000 22.000000 32.000000 68.000000
V284 V285 V286 V287 \
count 590528.000000 590528.000000 590528.000000 590528.000000
mean 0.088543 1.167660 0.031492 0.358579
std 0.338424 3.282454 0.190939 1.078995
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 1.000000 0.000000 0.000000
max 12.000000 95.000000 8.000000 31.000000
V288 V289 V290 V291 \
count 589271.000000 589271.000000 590528.000000 590528.000000
mean 0.184350 0.235975 1.103011 1.659811
std 0.430989 0.599231 0.768897 16.252538
min 0.000000 0.000000 1.000000 1.000000
25% 0.000000 0.000000 1.000000 1.000000
50% 0.000000 0.000000 1.000000 1.000000
75% 0.000000 0.000000 1.000000 1.000000
max 10.000000 12.000000 67.000000 1055.000000
V292 V293 V294 V295 \
count 590528.000000 590528.000000 590528.000000 590528.000000
mean 1.239916 0.942599 2.313863 1.433424
std 3.775050 20.588816 39.526468 25.962948
min 1.000000 0.000000 0.000000 0.000000
25% 1.000000 0.000000 0.000000 0.000000
50% 1.000000 0.000000 0.000000 0.000000
75% 1.000000 0.000000 0.000000 0.000000
max 323.000000 869.000000 1286.000000 928.000000
V296 V297 V298 V299 \
count 589271.000000 590528.000000 590528.000000 590528.000000
mean 0.328917 0.089034 0.298829 0.171655
std 3.264745 0.628352 3.175062 1.724218
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 93.000000 12.000000 93.000000 49.000000
V300 V301 V302 V303 \
count 589271.000000 589271.000000 590528.000000 590528.000000
mean 0.045507 0.052002 0.251761 0.283140
std 0.289573 0.318310 0.481889 0.623608
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 11.000000 13.000000 16.000000 20.000000
V304 V305 V306 V307 \
count 590528.000000 590528.000000 590528.000000 590528.000000
mean 0.264208 1.000007 139.748713 408.682375
std 0.528238 0.002603 2348.849634 4391.992977
min 0.000000 1.000000 0.000000 0.000000
25% 0.000000 1.000000 0.000000 0.000000
50% 0.000000 1.000000 0.000000 0.000000
75% 0.000000 1.000000 0.000000 151.380680
max 16.000000 2.000000 108800.000000 145765.000000
V308 V309 V310 V311 \
count 590528.000000 590528.000000 590528.000000 590528.000000
mean 230.413180 10.995986 118.195658 4.202175
std 3021.924247 116.254277 352.983093 102.374938
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 35.970001 0.000000 107.949997 0.000000
max 108800.000000 55125.000000 55125.000000 55125.000000
V312 V313 V314 V315 \
count 590528.000000 589271.000000 589271.000000 589271.000000
mean 39.173910 21.351473 43.319174 26.806977
std 172.128339 95.902970 173.619028 116.853222
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 55125.000000 4817.470215 7519.870117 4817.470215
V316 V317 V318 V319 \
count 590528.000000 590528.000000 590528.000000 590528.000000
mean 109.818544 247.606741 162.153398 18.372476
std 2270.033202 3980.042828 2793.343636 332.304848
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 93736.000000 134021.000000 98476.000000 104060.000000
V320 V321 V322 V323 V324 \
count 590528.000000 590528.000000 82351.000000 82351.000000 82351.000000
mean 42.073133 28.326584 6.220289 13.103775 9.184612
std 473.499307 382.053171 56.022561 106.739813 73.627893
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 1.000000 0.000000
max 104060.000000 104060.000000 880.000000 1411.000000 976.000000
V325 V326 V327 V328 V329 \
count 82351.000000 82351.000000 82351.000000 82351.000000 82351.000000
mean 0.058494 0.851040 0.296633 0.336790 1.312844
std 0.304415 3.950295 1.364356 1.580144 8.769083
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000 0.000000
max 12.000000 44.000000 18.000000 15.000000 99.000000
V330 V331 V332 V333 \
count 82351.000000 82351.000000 82351.000000 82351.000000
mean 0.775874 721.741883 1375.783644 1014.622782
std 4.727971 6217.223583 11169.275702 7955.735482
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 25.000000 0.000000
max 55.000000 160000.000000 160000.000000 160000.000000
V334 V335 V336 V337 V338 \
count 82351.000000 82351.00000 82351.000000 82351.000000 82351.000000
mean 9.807015 59.16455 28.530903 55.352422 151.160542
std 243.861391 387.62948 274.576920 668.486833 1095.034387
min 0.000000 0.00000 0.000000 0.000000 0.000000
25% 0.000000 0.00000 0.000000 0.000000 0.000000
50% 0.000000 0.00000 0.000000 0.000000 0.000000
75% 0.000000 0.00000 0.000000 0.000000 0.000000
max 55125.000000 55125.00000 55125.000000 104060.000000 104060.000000
V339
count 82351.000000
mean 100.700882
std 814.946722
min 0.000000
25% 0.000000
50% 0.000000
75% 0.000000
max 104060.000000
Identity dataset
TransactionID id_01 id_02 id_03 \
count 1.442330e+05 144233.000000 140872.000000 66324.000000
mean 3.236329e+06 -10.170502 174716.584708 0.060189
std 1.788496e+05 14.347949 159651.816856 0.598231
min 2.987004e+06 -100.000000 1.000000 -13.000000
25% 3.077142e+06 -10.000000 67992.000000 0.000000
50% 3.198818e+06 -5.000000 125800.500000 0.000000
75% 3.392923e+06 -5.000000 228749.000000 0.000000
max 3.577534e+06 0.000000 999595.000000 10.000000
id_04 id_05 id_06 id_07 id_08 \
count 66324.000000 136865.000000 136865.000000 5155.000000 5155.000000
mean -0.058938 1.615585 -6.698710 13.285354 -38.600388
std 0.701015 5.249856 16.491104 11.384207 26.084899
min -28.000000 -72.000000 -100.000000 -46.000000 -100.000000
25% 0.000000 0.000000 -6.000000 5.000000 -48.000000
50% 0.000000 0.000000 0.000000 14.000000 -34.000000
75% 0.000000 1.000000 0.000000 22.000000 -23.000000
max 0.000000 52.000000 0.000000 61.000000 0.000000
id_09 id_10 id_11 id_13 id_14 \
count 74926.000000 74926.000000 140978.000000 127320.000000 80044.000000
mean 0.091023 -0.301124 99.745325 48.053071 -344.507146
std 0.983842 2.789446 1.127602 11.774858 93.695502
min -36.000000 -100.000000 90.000000 10.000000 -660.000000
25% 0.000000 0.000000 100.000000 49.000000 -360.000000
50% 0.000000 0.000000 100.000000 52.000000 -300.000000
75% 0.000000 0.000000 100.000000 52.000000 -300.000000
max 25.000000 0.000000 100.000000 64.000000 720.000000
id_17 id_18 id_19 id_20 id_21 \
count 139369.000000 45113.000000 139318.000000 139261.000000 5159.000000
mean 189.451377 14.237337 353.128174 403.882666 368.269820
std 30.375360 1.561302 141.095343 152.160327 198.847038
min 100.000000 10.000000 100.000000 100.000000 100.000000
25% 166.000000 13.000000 266.000000 256.000000 252.000000
50% 166.000000 15.000000 341.000000 472.000000 252.000000
75% 225.000000 15.000000 427.000000 533.000000 486.500000
max 229.000000 29.000000 671.000000 661.000000 854.000000
id_22 id_24 id_25 id_26 id_32
count 5169.000000 4747.000000 5132.000000 5163.000000 77586.000000
mean 16.002708 12.800927 329.608924 149.070308 26.508597
std 6.897665 2.372447 97.461089 32.101995 3.737502
min 10.000000 11.000000 100.000000 100.000000 0.000000
25% 14.000000 11.000000 321.000000 119.000000 24.000000
50% 14.000000 11.000000 321.000000 149.000000 24.000000
75% 14.000000 15.000000 371.000000 169.000000 32.000000
max 44.000000 26.000000 548.000000 216.000000 32.000000
# List the columns in each dataset.
print(list(transaction.columns))
print(list(identity.columns))
['TransactionID', 'isFraud', 'TransactionDT', 'TransactionAmt', 'ProductCD', 'card1', 'card2', 'card3', 'card4', 'card5', 'card6', 'addr1', 'addr2', 'dist1', 'dist2', 'P_emaildomain', 'R_emaildomain', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9', 'C10', 'C11', 'C12', 'C13', 'C14', 'D1', 'D2', 'D3', 'D4', 'D5', 'D6', 'D7', 'D8', 'D9', 'D10', 'D11', 'D12', 'D13', 'D14', 'D15', 'M1', 'M2', 'M3', 'M4', 'M5', 'M6', 'M7', 'M8', 'M9', 'V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10', 'V11', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20', 'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'V29', 'V30', 'V31', 'V32', 'V33', 'V34', 'V35', 'V36', 'V37', 'V38', 'V39', 'V40', 'V41', 'V42', 'V43', 'V44', 'V45', 'V46', 'V47', 'V48', 'V49', 'V50', 'V51', 'V52', 'V53', 'V54', 'V55', 'V56', 'V57', 'V58', 'V59', 'V60', 'V61', 'V62', 'V63', 'V64', 'V65', 'V66', 'V67', 'V68', 'V69', 'V70', 'V71', 'V72', 'V73', 'V74', 'V75', 'V76', 'V77', 'V78', 'V79', 'V80', 'V81', 'V82', 'V83', 'V84', 'V85', 'V86', 'V87', 'V88', 'V89', 'V90', 'V91', 'V92', 'V93', 'V94', 'V95', 'V96', 'V97', 'V98', 'V99', 'V100', 'V101', 'V102', 'V103', 'V104', 'V105', 'V106', 'V107', 'V108', 'V109', 'V110', 'V111', 'V112', 'V113', 'V114', 'V115', 'V116', 'V117', 'V118', 'V119', 'V120', 'V121', 'V122', 'V123', 'V124', 'V125', 'V126', 'V127', 'V128', 'V129', 'V130', 'V131', 'V132', 'V133', 'V134', 'V135', 'V136', 'V137', 'V138', 'V139', 'V140', 'V141', 'V142', 'V143', 'V144', 'V145', 'V146', 'V147', 'V148', 'V149', 'V150', 'V151', 'V152', 'V153', 'V154', 'V155', 'V156', 'V157', 'V158', 'V159', 'V160', 'V161', 'V162', 'V163', 'V164', 'V165', 'V166', 'V167', 'V168', 'V169', 'V170', 'V171', 'V172', 'V173', 'V174', 'V175', 'V176', 'V177', 'V178', 'V179', 'V180', 'V181', 'V182', 'V183', 'V184', 'V185', 'V186', 'V187', 'V188', 'V189', 'V190', 'V191', 'V192', 'V193', 'V194', 'V195', 'V196', 'V197', 'V198', 'V199', 'V200', 'V201', 'V202', 'V203', 'V204', 'V205', 'V206', 'V207', 'V208', 'V209', 'V210', 'V211', 'V212', 'V213', 'V214', 'V215', 'V216', 'V217', 'V218', 'V219', 'V220', 'V221', 'V222', 'V223', 'V224', 'V225', 'V226', 'V227', 'V228', 'V229', 'V230', 'V231', 'V232', 'V233', 'V234', 'V235', 'V236', 'V237', 'V238', 'V239', 'V240', 'V241', 'V242', 'V243', 'V244', 'V245', 'V246', 'V247', 'V248', 'V249', 'V250', 'V251', 'V252', 'V253', 'V254', 'V255', 'V256', 'V257', 'V258', 'V259', 'V260', 'V261', 'V262', 'V263', 'V264', 'V265', 'V266', 'V267', 'V268', 'V269', 'V270', 'V271', 'V272', 'V273', 'V274', 'V275', 'V276', 'V277', 'V278', 'V279', 'V280', 'V281', 'V282', 'V283', 'V284', 'V285', 'V286', 'V287', 'V288', 'V289', 'V290', 'V291', 'V292', 'V293', 'V294', 'V295', 'V296', 'V297', 'V298', 'V299', 'V300', 'V301', 'V302', 'V303', 'V304', 'V305', 'V306', 'V307', 'V308', 'V309', 'V310', 'V311', 'V312', 'V313', 'V314', 'V315', 'V316', 'V317', 'V318', 'V319', 'V320', 'V321', 'V322', 'V323', 'V324', 'V325', 'V326', 'V327', 'V328', 'V329', 'V330', 'V331', 'V332', 'V333', 'V334', 'V335', 'V336', 'V337', 'V338', 'V339']
['TransactionID', 'id_01', 'id_02', 'id_03', 'id_04', 'id_05', 'id_06', 'id_07', 'id_08', 'id_09', 'id_10', 'id_11', 'id_12', 'id_13', 'id_14', 'id_15', 'id_16', 'id_17', 'id_18', 'id_19', 'id_20', 'id_21', 'id_22', 'id_23', 'id_24', 'id_25', 'id_26', 'id_27', 'id_28', 'id_29', 'id_30', 'id_31', 'id_32', 'id_33', 'id_34', 'id_35', 'id_36', 'id_37', 'id_38', 'DeviceType', 'DeviceInfo']
# Check the proportion of fraud to non-fraud observations in the
# transaction dataset.
# Fraudulent transactions are represented by 'isFraud' = 1
# and non-fraudulent transactions are represented by 'isFraud' = 0.
fraud = sum(transaction['isFraud'])
not_fraud = len(transaction.index)-fraud
percent_fraud = fraud/(fraud+not_fraud)
print('There are '+'{:,.0f}'.format(fraud)+' fraudulent transactions out of '+
'{:,.0f}'.format(fraud+not_fraud)+' total transactions in the dataset.')
print('These fraudulent transactions represent approximately '+'{:,.2%}'.format(percent_fraud)+
' of all transactions.')
There are 20,663 fraudulent transactions out of 590,540 total transactions in the dataset.
These fraudulent transactions represent approximately 3.50% of all transactions.
The following information about the datasets is noted:
the transaction dataset has 590,540 observations and 394 columns;
the response in the transaction dataset is ‘isFraud’;
approximately 3.5% of all transactions are fraudulent transactions;
the identity dataset has 144,233 observations and 40 columns; and
the ‘Transaction_ID’ column can be used as a key to link the transaction and identity datasets together.
# Examine how fraud transactions compare to non fraud transactions
# across some of the features.
# Calculate the average transaction amounts for fraud and non fraud transactions.
heading('Average transaction amounts for fraud and non fraud')
print(transaction.groupby('isFraud').mean()['TransactionAmt'])
print('\n')
# Calculate percentage fraud for each Product Code.
heading('Percentage fraud and total transactions for each Product Code')
product_groups = transaction[['ProductCD','isFraud']].groupby('ProductCD').agg(['mean','count'])
print(product_groups)
Average transaction amounts for fraud and non fraud
isFraud
0 134.511665
1 149.244779
Name: TransactionAmt, dtype: float64
Percentage fraud and total transactions for each Product Code
isFraud
mean count
ProductCD
C 0.116873 68519
H 0.047662 33024
R 0.037826 37699
S 0.058996 11628
W 0.020399 439670
The average transaction amount is slightly higher for fraud cases (\(149 v \)135).
The percentage of transactions that are fraudulent is quite different by product code. The fraud percentage is greatest for product code ‘C’ (11.7%) and smallest for product code ‘W’ (2%). These different fraud percentages for different product codes suggest that it might be helpful to look at instances of fraud separately for each of the 5 product codes.
The rest of this case study will focus on fraud for product code ‘C’.
You could then repeat the analysis below for each of the other product codes.
Prepare data#
# Join the transaction and identity datasets using a left join so that all
# observations in the transaction dataset are retained
# (the transaction dataset contains the response 'isFraud'), and any matching
# observations in the identity dataset are joined into the merge.
product = 'C'
fraud_data = pd.merge(transaction[transaction['ProductCD']=='C'],identity,on='TransactionID',how='left')
print(fraud_data.info())
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Columns: 434 entries, TransactionID to DeviceInfo
dtypes: float64(399), int64(4), object(31)
memory usage: 227.4+ MB
None
The fraud dataset created above contains 68,519 observations of fraud for the product being investigated (product code ‘C’) and 434 columns (‘TransactionID’, ‘isFraud’ and 432 features).
The number of features should be reduced to make the model fitting more tractable.
The features used in the clustering algorithm should be numeric and not contain missing values, so that Euclidean distances between the observations can be calculated.
# Explore the feature types and missingness of the fraud data.
# Explore the first 14 features.
print(fraud_data[['TransactionDT','TransactionAmt','card1','card2','card3','card4',
'card5','card6','addr1','addr2','dist1','dist2']].info())
# Explore the 'C#' features.
filter_col = [col for col in fraud_data if col.startswith('C')]
print(fraud_data[filter_col].info())
# Explore the 'D#' features.
filter_col = [col for col in fraud_data if col.startswith('D')]
print(fraud_data[filter_col].info())
# Explore the 'M#' features.
filter_col = [col for col in fraud_data if col.startswith('M')]
print(fraud_data[filter_col].info())
# Explore the first 100 'V#' features.
filter_col = [col for col in fraud_data if col.startswith('V')][0:100]
print(fraud_data[filter_col].info())
# Explore the next 100 'V#' features.
filter_col = [col for col in fraud_data if col.startswith('V')][100:200]
print(fraud_data[filter_col].info())
# Explore the next 100 'V#' features.
filter_col = [col for col in fraud_data if col.startswith('V')][200:300]
print(fraud_data[filter_col].info())
# Explore the final 39 'V#' features.
filter_col = [col for col in fraud_data if col.startswith('V')][300:]
print(fraud_data[filter_col].info())
# Explore the id_## features.
filter_col = [col for col in fraud_data if col.startswith('id')]
print(fraud_data[filter_col].info())
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 TransactionDT 68519 non-null int64
1 TransactionAmt 68519 non-null float64
2 card1 68519 non-null int64
3 card2 67988 non-null float64
4 card3 68326 non-null float64
5 card4 68324 non-null object
6 card5 67896 non-null float64
7 card6 68326 non-null object
8 addr1 3400 non-null float64
9 addr2 3400 non-null float64
10 dist1 0 non-null float64
11 dist2 26741 non-null float64
dtypes: float64(8), int64(2), object(2)
memory usage: 6.8+ MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 C1 68519 non-null float64
1 C2 68519 non-null float64
2 C3 68519 non-null float64
3 C4 68519 non-null float64
4 C5 68519 non-null float64
5 C6 68519 non-null float64
6 C7 68519 non-null float64
7 C8 68519 non-null float64
8 C9 68519 non-null float64
9 C10 68519 non-null float64
10 C11 68519 non-null float64
11 C12 68519 non-null float64
12 C13 68519 non-null float64
13 C14 68519 non-null float64
dtypes: float64(14)
memory usage: 7.8 MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 17 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 D1 68324 non-null float64
1 D2 20184 non-null float64
2 D3 26800 non-null float64
3 D4 64356 non-null float64
4 D5 32584 non-null float64
5 D6 64352 non-null float64
6 D7 32503 non-null float64
7 D8 29436 non-null float64
8 D9 29436 non-null float64
9 D10 65021 non-null float64
10 D11 0 non-null float64
11 D12 64717 non-null float64
12 D13 57948 non-null float64
13 D14 51083 non-null float64
14 D15 64581 non-null float64
15 DeviceType 61015 non-null object
16 DeviceInfo 41593 non-null object
dtypes: float64(15), object(2)
memory usage: 9.4+ MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 M1 0 non-null object
1 M2 0 non-null object
2 M3 0 non-null object
3 M4 66785 non-null object
4 M5 0 non-null object
5 M6 0 non-null object
6 M7 0 non-null object
7 M8 0 non-null object
8 M9 0 non-null object
dtypes: object(9)
memory usage: 5.2+ MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 100 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V1 0 non-null float64
1 V2 0 non-null float64
2 V3 0 non-null float64
3 V4 0 non-null float64
4 V5 0 non-null float64
5 V6 0 non-null float64
6 V7 0 non-null float64
7 V8 0 non-null float64
8 V9 0 non-null float64
9 V10 0 non-null float64
10 V11 0 non-null float64
11 V12 65021 non-null float64
12 V13 65021 non-null float64
13 V14 65021 non-null float64
14 V15 65021 non-null float64
15 V16 65021 non-null float64
16 V17 65021 non-null float64
17 V18 65021 non-null float64
18 V19 65021 non-null float64
19 V20 65021 non-null float64
20 V21 65021 non-null float64
21 V22 65021 non-null float64
22 V23 65021 non-null float64
23 V24 65021 non-null float64
24 V25 65021 non-null float64
25 V26 65021 non-null float64
26 V27 65021 non-null float64
27 V28 65021 non-null float64
28 V29 65021 non-null float64
29 V30 65021 non-null float64
30 V31 65021 non-null float64
31 V32 65021 non-null float64
32 V33 65021 non-null float64
33 V34 65021 non-null float64
34 V35 64356 non-null float64
35 V36 64356 non-null float64
36 V37 64356 non-null float64
37 V38 64356 non-null float64
38 V39 64356 non-null float64
39 V40 64356 non-null float64
40 V41 64356 non-null float64
41 V42 64356 non-null float64
42 V43 64356 non-null float64
43 V44 64356 non-null float64
44 V45 64356 non-null float64
45 V46 64356 non-null float64
46 V47 64356 non-null float64
47 V48 64356 non-null float64
48 V49 64356 non-null float64
49 V50 64356 non-null float64
50 V51 64356 non-null float64
51 V52 64356 non-null float64
52 V53 67067 non-null float64
53 V54 67067 non-null float64
54 V55 67067 non-null float64
55 V56 67067 non-null float64
56 V57 67067 non-null float64
57 V58 67067 non-null float64
58 V59 67067 non-null float64
59 V60 67067 non-null float64
60 V61 67067 non-null float64
61 V62 67067 non-null float64
62 V63 67067 non-null float64
63 V64 67067 non-null float64
64 V65 67067 non-null float64
65 V66 67067 non-null float64
66 V67 67067 non-null float64
67 V68 67067 non-null float64
68 V69 67067 non-null float64
69 V70 67067 non-null float64
70 V71 67067 non-null float64
71 V72 67067 non-null float64
72 V73 67067 non-null float64
73 V74 67067 non-null float64
74 V75 64581 non-null float64
75 V76 64581 non-null float64
76 V77 64581 non-null float64
77 V78 64581 non-null float64
78 V79 64581 non-null float64
79 V80 64581 non-null float64
80 V81 64581 non-null float64
81 V82 64581 non-null float64
82 V83 64581 non-null float64
83 V84 64581 non-null float64
84 V85 64581 non-null float64
85 V86 64581 non-null float64
86 V87 64581 non-null float64
87 V88 64581 non-null float64
88 V89 64581 non-null float64
89 V90 64581 non-null float64
90 V91 64581 non-null float64
91 V92 64581 non-null float64
92 V93 64581 non-null float64
93 V94 64581 non-null float64
94 V95 68447 non-null float64
95 V96 68447 non-null float64
96 V97 68447 non-null float64
97 V98 68447 non-null float64
98 V99 68447 non-null float64
99 V100 68447 non-null float64
dtypes: float64(100)
memory usage: 52.8 MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 100 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V101 68447 non-null float64
1 V102 68447 non-null float64
2 V103 68447 non-null float64
3 V104 68447 non-null float64
4 V105 68447 non-null float64
5 V106 68447 non-null float64
6 V107 68447 non-null float64
7 V108 68447 non-null float64
8 V109 68447 non-null float64
9 V110 68447 non-null float64
10 V111 68447 non-null float64
11 V112 68447 non-null float64
12 V113 68447 non-null float64
13 V114 68447 non-null float64
14 V115 68447 non-null float64
15 V116 68447 non-null float64
16 V117 68447 non-null float64
17 V118 68447 non-null float64
18 V119 68447 non-null float64
19 V120 68447 non-null float64
20 V121 68447 non-null float64
21 V122 68447 non-null float64
22 V123 68447 non-null float64
23 V124 68447 non-null float64
24 V125 68447 non-null float64
25 V126 68447 non-null float64
26 V127 68447 non-null float64
27 V128 68447 non-null float64
28 V129 68447 non-null float64
29 V130 68447 non-null float64
30 V131 68447 non-null float64
31 V132 68447 non-null float64
32 V133 68447 non-null float64
33 V134 68447 non-null float64
34 V135 68447 non-null float64
35 V136 68447 non-null float64
36 V137 68447 non-null float64
37 V138 0 non-null float64
38 V139 0 non-null float64
39 V140 0 non-null float64
40 V141 0 non-null float64
41 V142 0 non-null float64
42 V143 0 non-null float64
43 V144 0 non-null float64
44 V145 0 non-null float64
45 V146 0 non-null float64
46 V147 0 non-null float64
47 V148 0 non-null float64
48 V149 0 non-null float64
49 V150 0 non-null float64
50 V151 0 non-null float64
51 V152 0 non-null float64
52 V153 0 non-null float64
53 V154 0 non-null float64
54 V155 0 non-null float64
55 V156 0 non-null float64
56 V157 0 non-null float64
57 V158 0 non-null float64
58 V159 0 non-null float64
59 V160 0 non-null float64
60 V161 0 non-null float64
61 V162 0 non-null float64
62 V163 0 non-null float64
63 V164 0 non-null float64
64 V165 0 non-null float64
65 V166 0 non-null float64
66 V167 59669 non-null float64
67 V168 59669 non-null float64
68 V169 59885 non-null float64
69 V170 59885 non-null float64
70 V171 59885 non-null float64
71 V172 59669 non-null float64
72 V173 59669 non-null float64
73 V174 59885 non-null float64
74 V175 59885 non-null float64
75 V176 59669 non-null float64
76 V177 59669 non-null float64
77 V178 59669 non-null float64
78 V179 59669 non-null float64
79 V180 59885 non-null float64
80 V181 59669 non-null float64
81 V182 59669 non-null float64
82 V183 59669 non-null float64
83 V184 59885 non-null float64
84 V185 59885 non-null float64
85 V186 59669 non-null float64
86 V187 59669 non-null float64
87 V188 59885 non-null float64
88 V189 59885 non-null float64
89 V190 59669 non-null float64
90 V191 59669 non-null float64
91 V192 59669 non-null float64
92 V193 59669 non-null float64
93 V194 59885 non-null float64
94 V195 59885 non-null float64
95 V196 59669 non-null float64
96 V197 59885 non-null float64
97 V198 59885 non-null float64
98 V199 59669 non-null float64
99 V200 59885 non-null float64
dtypes: float64(100)
memory usage: 52.8 MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 100 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V201 59885 non-null float64
1 V202 59669 non-null float64
2 V203 59669 non-null float64
3 V204 59669 non-null float64
4 V205 59669 non-null float64
5 V206 59669 non-null float64
6 V207 59669 non-null float64
7 V208 59885 non-null float64
8 V209 59885 non-null float64
9 V210 59885 non-null float64
10 V211 59669 non-null float64
11 V212 59669 non-null float64
12 V213 59669 non-null float64
13 V214 59669 non-null float64
14 V215 59669 non-null float64
15 V216 59669 non-null float64
16 V217 52036 non-null float64
17 V218 52036 non-null float64
18 V219 52036 non-null float64
19 V220 59160 non-null float64
20 V221 59160 non-null float64
21 V222 59160 non-null float64
22 V223 52036 non-null float64
23 V224 52036 non-null float64
24 V225 52036 non-null float64
25 V226 52036 non-null float64
26 V227 59160 non-null float64
27 V228 52036 non-null float64
28 V229 52036 non-null float64
29 V230 52036 non-null float64
30 V231 52036 non-null float64
31 V232 52036 non-null float64
32 V233 52036 non-null float64
33 V234 59160 non-null float64
34 V235 52036 non-null float64
35 V236 52036 non-null float64
36 V237 52036 non-null float64
37 V238 59160 non-null float64
38 V239 59160 non-null float64
39 V240 52036 non-null float64
40 V241 52036 non-null float64
41 V242 52036 non-null float64
42 V243 52036 non-null float64
43 V244 52036 non-null float64
44 V245 59160 non-null float64
45 V246 52036 non-null float64
46 V247 52036 non-null float64
47 V248 52036 non-null float64
48 V249 52036 non-null float64
49 V250 59160 non-null float64
50 V251 59160 non-null float64
51 V252 52036 non-null float64
52 V253 52036 non-null float64
53 V254 52036 non-null float64
54 V255 59160 non-null float64
55 V256 59160 non-null float64
56 V257 52036 non-null float64
57 V258 52036 non-null float64
58 V259 59160 non-null float64
59 V260 52036 non-null float64
60 V261 52036 non-null float64
61 V262 52036 non-null float64
62 V263 52036 non-null float64
63 V264 52036 non-null float64
64 V265 52036 non-null float64
65 V266 52036 non-null float64
66 V267 52036 non-null float64
67 V268 52036 non-null float64
68 V269 52036 non-null float64
69 V270 59160 non-null float64
70 V271 59160 non-null float64
71 V272 59160 non-null float64
72 V273 52036 non-null float64
73 V274 52036 non-null float64
74 V275 52036 non-null float64
75 V276 52036 non-null float64
76 V277 52036 non-null float64
77 V278 52036 non-null float64
78 V279 68512 non-null float64
79 V280 68512 non-null float64
80 V281 68324 non-null float64
81 V282 68324 non-null float64
82 V283 68324 non-null float64
83 V284 68512 non-null float64
84 V285 68512 non-null float64
85 V286 68512 non-null float64
86 V287 68512 non-null float64
87 V288 68324 non-null float64
88 V289 68324 non-null float64
89 V290 68512 non-null float64
90 V291 68512 non-null float64
91 V292 68512 non-null float64
92 V293 68512 non-null float64
93 V294 68512 non-null float64
94 V295 68512 non-null float64
95 V296 68324 non-null float64
96 V297 68512 non-null float64
97 V298 68512 non-null float64
98 V299 68512 non-null float64
99 V300 68324 non-null float64
dtypes: float64(100)
memory usage: 52.8 MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 39 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V301 68324 non-null float64
1 V302 68512 non-null float64
2 V303 68512 non-null float64
3 V304 68512 non-null float64
4 V305 68512 non-null float64
5 V306 68512 non-null float64
6 V307 68512 non-null float64
7 V308 68512 non-null float64
8 V309 68512 non-null float64
9 V310 68512 non-null float64
10 V311 68512 non-null float64
11 V312 68512 non-null float64
12 V313 68324 non-null float64
13 V314 68324 non-null float64
14 V315 68324 non-null float64
15 V316 68512 non-null float64
16 V317 68512 non-null float64
17 V318 68512 non-null float64
18 V319 68512 non-null float64
19 V320 68512 non-null float64
20 V321 68512 non-null float64
21 V322 0 non-null float64
22 V323 0 non-null float64
23 V324 0 non-null float64
24 V325 0 non-null float64
25 V326 0 non-null float64
26 V327 0 non-null float64
27 V328 0 non-null float64
28 V329 0 non-null float64
29 V330 0 non-null float64
30 V331 0 non-null float64
31 V332 0 non-null float64
32 V333 0 non-null float64
33 V334 0 non-null float64
34 V335 0 non-null float64
35 V336 0 non-null float64
36 V337 0 non-null float64
37 V338 0 non-null float64
38 V339 0 non-null float64
dtypes: float64(39)
memory usage: 20.9 MB
None
<class 'pandas.core.frame.DataFrame'>
Int64Index: 68519 entries, 0 to 68518
Data columns (total 38 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id_01 62192 non-null float64
1 id_02 61015 non-null float64
2 id_03 27141 non-null float64
3 id_04 27141 non-null float64
4 id_05 59809 non-null float64
5 id_06 59809 non-null float64
6 id_07 491 non-null float64
7 id_08 491 non-null float64
8 id_09 29436 non-null float64
9 id_10 29436 non-null float64
10 id_11 61016 non-null float64
11 id_12 62192 non-null object
12 id_13 60121 non-null float64
13 id_14 2396 non-null float64
14 id_15 61016 non-null object
15 id_16 51136 non-null object
16 id_17 60724 non-null float64
17 id_18 15052 non-null float64
18 id_19 60701 non-null float64
19 id_20 60656 non-null float64
20 id_21 495 non-null float64
21 id_22 495 non-null float64
22 id_23 495 non-null object
23 id_24 274 non-null float64
24 id_25 484 non-null float64
25 id_26 494 non-null float64
26 id_27 495 non-null object
27 id_28 61016 non-null object
28 id_29 61016 non-null object
29 id_30 0 non-null object
30 id_31 60898 non-null object
31 id_32 0 non-null float64
32 id_33 0 non-null object
33 id_34 0 non-null object
34 id_35 61016 non-null object
35 id_36 61016 non-null object
36 id_37 61016 non-null object
37 id_38 61016 non-null object
dtypes: float64(23), object(15)
memory usage: 20.4+ MB
None
Based on the information above, the number of features could be reduced by only selecting those that are numeric and have at least 60,000 observations.
# Select the features that are numeric and have at least 60,000 observations.
fraud_numeric = fraud_data.select_dtypes(['number']).drop(columns='TransactionID')
# Select only the features that have at least 60,000 non-missing values.
fraud_numeric2 = pd.DataFrame()
for (columnName, columnData) in fraud_numeric.iteritems():
enough_data = columnData.notna().sum() > 60000
if enough_data:
fraud_numeric2[columnName] = columnData
# Then select only the rows that do not have any missing values.
fraud_numeric3 = fraud_numeric2.dropna(axis='rows')
print(fraud_numeric3.info())
print(list(fraud_numeric3.columns))
# Check that there are no missing values in this new fraud data
print('There are '+str(fraud_numeric3.isna().sum().sum())+' missing values')
<class 'pandas.core.frame.DataFrame'>
Int64Index: 51660 entries, 0 to 68518
Columns: 203 entries, isFraud to id_20
dtypes: float64(200), int64(3)
memory usage: 80.4 MB
None
['isFraud', 'TransactionDT', 'TransactionAmt', 'card1', 'card2', 'card3', 'card5', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9', 'C10', 'C11', 'C12', 'C13', 'C14', 'D1', 'D4', 'D6', 'D10', 'D12', 'D15', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20', 'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'V29', 'V30', 'V31', 'V32', 'V33', 'V34', 'V35', 'V36', 'V37', 'V38', 'V39', 'V40', 'V41', 'V42', 'V43', 'V44', 'V45', 'V46', 'V47', 'V48', 'V49', 'V50', 'V51', 'V52', 'V53', 'V54', 'V55', 'V56', 'V57', 'V58', 'V59', 'V60', 'V61', 'V62', 'V63', 'V64', 'V65', 'V66', 'V67', 'V68', 'V69', 'V70', 'V71', 'V72', 'V73', 'V74', 'V75', 'V76', 'V77', 'V78', 'V79', 'V80', 'V81', 'V82', 'V83', 'V84', 'V85', 'V86', 'V87', 'V88', 'V89', 'V90', 'V91', 'V92', 'V93', 'V94', 'V95', 'V96', 'V97', 'V98', 'V99', 'V100', 'V101', 'V102', 'V103', 'V104', 'V105', 'V106', 'V107', 'V108', 'V109', 'V110', 'V111', 'V112', 'V113', 'V114', 'V115', 'V116', 'V117', 'V118', 'V119', 'V120', 'V121', 'V122', 'V123', 'V124', 'V125', 'V126', 'V127', 'V128', 'V129', 'V130', 'V131', 'V132', 'V133', 'V134', 'V135', 'V136', 'V137', 'V279', 'V280', 'V281', 'V282', 'V283', 'V284', 'V285', 'V286', 'V287', 'V288', 'V289', 'V290', 'V291', 'V292', 'V293', 'V294', 'V295', 'V296', 'V297', 'V298', 'V299', 'V300', 'V301', 'V302', 'V303', 'V304', 'V305', 'V306', 'V307', 'V308', 'V309', 'V310', 'V311', 'V312', 'V313', 'V314', 'V315', 'V316', 'V317', 'V318', 'V319', 'V320', 'V321', 'id_01', 'id_02', 'id_11', 'id_13', 'id_17', 'id_19', 'id_20']
There are 0 missing values
# Separate response ('isFraud') from features in the fraud data.
fraud_response = fraud_numeric3['isFraud']
fraud_features = fraud_numeric3.drop(columns=['isFraud'])
print(fraud_features.info())
<class 'pandas.core.frame.DataFrame'>
Int64Index: 51660 entries, 0 to 68518
Columns: 202 entries, TransactionDT to id_20
dtypes: float64(200), int64(2)
memory usage: 80.0 MB
None
The fraud data now contains 51,660 observations on 202 features with no missing values.
If fraud assessors who were familiar with this dataset were available to speak to, they could provide qualitative information about the features that are likely to be good predictors of fraud. This information could then be used to refine the feature selection process.
Assume that you have access to these fraud assessors and they have suggested you the following features might be the most helpful in identifying fraud:
id_02;
id_19;
id_20;
V44;
V45;
V86;
V87;
C1;
C2;
C8;
C11;
C12;
C13;
C14;
card1;
card2;
TransactionAmt; and
TransactionDT.
You will use this reduced feature list to perform your initial modelling.
# Reduce the feature list to those suggested above.
fraud_features_selected = fraud_features[['id_02', 'id_19', 'id_20',
'V44','V45', 'V86', 'V87',
'C1','C2', 'C8', 'C11', 'C12',
'C13', 'C14', 'card1', 'card2',
'TransactionAmt', 'TransactionDT']]
print(fraud_features_selected.head())
id_02 id_19 id_20 V44 V45 V86 V87 C1 C2 C8 C11 C12 C13 \
0 191631.0 410.0 142.0 1.0 1.0 1.0 1.0 1.0 4.0 1.0 2.0 2.0 2.0
1 221832.0 176.0 507.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
2 116098.0 410.0 142.0 2.0 2.0 2.0 2.0 2.0 5.0 1.0 2.0 2.0 3.0
3 257037.0 484.0 507.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
4 287959.0 254.0 507.0 1.0 1.0 1.0 1.0 1.0 2.0 2.0 1.0 1.0 2.0
C14 card1 card2 TransactionAmt TransactionDT
0 1.0 16496 352.0 75.887 86549
1 1.0 4461 375.0 16.495 86555
2 2.0 13329 569.0 75.887 87209
3 1.0 15885 545.0 42.294 87317
4 1.0 12730 266.0 3.595 87317
# Create a scaler so that the features in the dataset can be
# scaled to have a mean of 0 and a standard deviation of 1.
scaler = StandardScaler()
fraud_features_scaled = scaler.fit_transform(fraud_features_selected)
Modelling#
This section:
fits a model;
evaluates the fitted model;
improves the model; and
selects a final model.
Fit model#
# Perform K-means clustering on the fraud dataset.
# Create KMeans models with values of k in the range 1 to 9.
clusters = range(1, 10)
seed = 50
kmeans = [KMeans(n_clusters=k,random_state=seed) for k in clusters]
# Setting random_state to a fixed value makes sure that the same results are
# achieved each time the model is run for each value of K.
# Fit the models and create an elbow curve to help select a value of
# K that provides a good clustering outcome, wihtout overfitting the data.
# The cluster score for each value of k is calculated to determine
# the one that gives the best clustering outcome.
# The cluster score (WCSS) measures the (negative) sum of squared
# distances of observations to their closest cluster centroid,
# so a smaller score indicates a better clustering of the data.
# Note that this step may take a while to run as the kmeans model needs to be
# fitted 10 times.
score = [kmeans[k].fit(fraud_features_scaled).score(fraud_features_scaled) for
k in range(len(kmeans))]
# Plot the elbow curve.
plt.plot(clusters,score)
plt.xlabel('Number of clusters (K)')
plt.ylabel('Cluster score')
plt.title('Elbow curve')
plt.show()
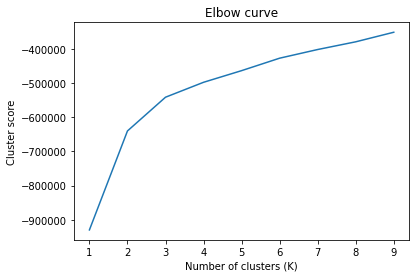
The elbow curve shows a slight ‘kink’ at K = 2 and another at K = 3, suggesting that these might be good values of K to use such that the clustering produces a small sum of squared distances but does not overfit the training data.
The model below will use a value of K = 3.
# Find outliers in the clusters to identify potential cases of fraud.
# The steps below will flag cases as fraud if they are far from their
# cluster centroid. In other words, they will be flagged as fraud if they
# look unusual compared to other observations in their cluster.
# Extract the selected kmeans model with K = 3 from the list of all
# kmeans models fitted.
# Note: because indexing starts at 0, the model with K = 3 has the list index 2.
kmeans_selected = kmeans[2]
# Get the cluster number for each observation in the fraud dataset.
labels = kmeans_selected.predict(fraud_features_scaled)
# Get the cluster centroids so that the distance from each observation to the
# centroid can be calculated to select cases to be flagged as fraud.
centroids = kmeans_selected.cluster_centers_
# Calculate the distance between each observation and its cluster centroid.
distance = [np.linalg.norm(X-Z) for X,Z in zip(fraud_features_scaled,centroids[labels])]
# np.linalg.norm is the 'norm' function from Numpy's linear algebra package
# and is used to calculate the Euclidean distance between two points,
# in this case between each observation (X) and its cluster centroid (Z).
# From the exploration of data above, it was seen that approximately 12% of
# Product Code C transactions were fraudulent. The code below will therefore
# classify an observation as fraudulent if its distance from its
# cluster centroid is above the 88th percentile of all distances in the cluster.
fraud_boundary = 88
fraud_prediction = np.array(distance)
fraud_prediction[distance>=np.percentile(distance, fraud_boundary)] = 1
# Assign an observation as being fraudulent (1) if it is outside the
# 88th percentile of observations in its cluster.
fraud_prediction[distance<np.percentile(distance, fraud_boundary)] = 0
# Otherwise assigne the observation as being non fraudulent (0).
print(fraud_prediction)
[0. 0. 1. ... 0. 1. 0.]
Evaluate model#
Unsupervised learning often involves working with datasets that do not contain response variable. In these cases, the output of a clustering algorithm can be evaluated using internal or manual evaluation techniques as described in Section 6.3.5 of Module 6.
An example of internal evaluation was shown above when the clustering scor (WCSS) was calculated based on the sum of squared distances between observations and their centroid clusters.
In fraud detection exercises, manual evaluation might be carried out by showing a fraud expert the observations in the training dataset that were classified as fraud and asking them to evaluate the likelihood that these observations were in fact fraud.
In this case study, response variables are available in the dataset, so these can be used to conduct external evaluation by comparing known cases of fraud to predicted cases of fraud. This external evaluation is performed below.
# Calculate and plot a confusion matrix to show True Positives, False Positives,
# True Negatives and False Negatives.
# Compute the confusion matrix.
cm = confusion_matrix(fraud_response, fraud_prediction)
# Plot the confusion matrix.
plot_confusion_matrix(cm, classes = ['Not fraud','Fraud'])
# Calculate the F1 score for these predictions.
# F1 = 2 x (precision * recall) / (precision + recall).
print('The F1 score is '+str(f1_score(fraud_response, fraud_prediction)))
The F1 score is 0.44971996990721397
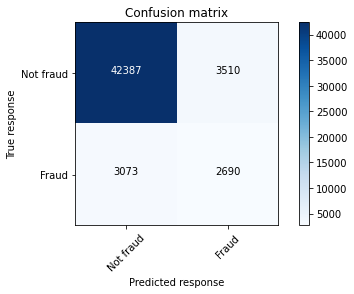
The confusion matrix shows that 2,690 (47%) of fraudulent transactions have been correctly classified as ‘Fraud’. It also shows that 3,510 (8%) of non fraudulent transactions that predicted to be fraud.
This suggests that there is room to improve the model to make it a more helpful tool for the fraud detection team to use.
Improve model#
The model might be improved by trying different values for the fraud_boundary or K, or by experimenting with different features used in the clustering.
The code below tries some different values for the fraud_boundary and K. You should also experiment to see if you can obtain better fraud predictions from the model, either by trying other values for fraud_coundary or K, or by trying different features to use in the clustering.
# Try different values for K.
# Extract the selected kmeans model with K = 4 from the list of all kmeans
# models fitted.
# Note: because indexing starts at 0, the model with K = 4 has the list index 3.
kmeans2 = kmeans[3]
# Get the cluster number for each observation in the fraud dataset.
labels2 = kmeans2.predict(fraud_features_scaled)
# Get the cluster centroids so that the distance from each observation to the
# centroid can be calculated to select cases to be flagged as fraud.
centroids2 = kmeans2.cluster_centers_
# Calculate the distance between each observation and the cluster centroid.
distance2 = [np.linalg.norm(X-Z) for X,Z in zip(fraud_features_scaled,
centroids2[labels2])]
# This time the fraud_boundary will be set to 80 so that more transactions will be
# identified as fraud.
fraud_boundary2 = 80
fraud_prediction2 = np.array(distance2)
fraud_prediction2[distance2>=np.percentile(distance2, fraud_boundary)] = 1
fraud_prediction2[distance2<np.percentile(distance2, fraud_boundary)] = 0
print(fraud_prediction2)
# Calculate and plot a confusion matrix to show True Positives, False Positives,
# True Negatives and False Negatives.
cm = confusion_matrix(fraud_response, fraud_prediction2)
plot_confusion_matrix(cm, classes = ['Not fraud','Fraud'])
# Compare the predictions from Kmeans1 and Kmeans2
{'KMeans1 F1':f1_score(fraud_response, fraud_prediction),
'KMeans2 F1':f1_score(fraud_response, fraud_prediction2),
}
[0. 0. 0. ... 0. 0. 0.]
{'KMeans1 F1': 0.44971996990721397, 'KMeans2 F1': 0.46225863077823287}
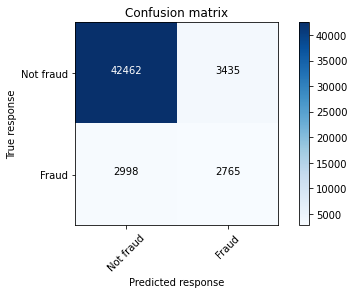
This model has a slightly higher F1 score, indicating it provides a slightly better fraud prediction than the original model.
Evaluation / observations#
This fraud detection model:
detects about 48% of true fraud cases in the training data (2,766 out of 5,763); and
classifies about 7.5% of true non-fraud cases in the training data as being fraudulent (3,434 out of 45,897).
Further, of the 6,200 transactions classified as fraud, only 45% of them are actual cases of fraud.
Therefore, this model probably requires further refinement to avoid missing too many true cases of fraud and to avoid classifying too many non-fraud cases as fraud.
It is likely that another classifier, such as a GBM or a neural network, would make better fraud predictions based on the training data. However, the power of the model presented above is that it does not need examples of fraud to be able to make a reasonable attempt at detecting them. This means that this ‘outlier’ classifier might be better at identifying new types of fraud that emerge over time than another classifier might be.
Further, while this case study has not provided a very good classification of fraudulent transactions based on the training data, it has demonstrated how clustering might be used to detect outliers in a dataset.
Afterword#
The output of fraud detection is a ‘short-list’ of possible outliers. Incorrectly accusing someone of fraudulent behaviour can have very detrimental financial and reputational impacts on an organisation, as well as likely causing the accused individual significant stress. For this reason, the results of a fraud detection activity usually need to be reviewed manually by a human to determine whether fraud has occurred or is likely to occur in each case. Further monitoring and/or investigation might be required before deciding whether fraud has occurred. Again, when conducting fraud investigations, it is important to consider the potential harm that can be caused to someone undergoing investigation.
At the same time, letting fraud go undetected and uncorrected can also be very costly for an organisation. Therefore, it is important to track how well any fraud detection algorithm performs over time. As the nature of fraud changes over time, it is important to assess whether the algorithm is keeping pace with the changing environment.
