SQL: Queries to Create Triangles#
This notebook was created by Jacky Poon for the Actuaries’ Analytical Cookbook.
Introduction and Setup#
This article describes a method with SQL to convert a transactional claims dataset to a triangle. With the source data often being in a data warehouse, by running queries in SQL we can efficiently extract a small summary set, rather than attempting to transfer what may be a large dataset of raw transactional data to our machine running Python or R. For this example, we will use Python for constructing our dummy dataset, and use duckdb as our SQL database, but basic concepts should apply similarly to other SQL databases.
There is also a dual purpose for this article to serve as an introduction to duckdb, a handy package that for running analytical SQL queries locally without having to use a data warehouse server.
!pip install duckdb
!pip show duckdb
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Collecting duckdb
Downloading duckdb-0.4.0-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (15.7 MB)
|████████████████████████████████| 15.7 MB 7.1 MB/s
?25hRequirement already satisfied: numpy>=1.14 in /usr/local/lib/python3.7/dist-packages (from duckdb) (1.21.6)
Installing collected packages: duckdb
Successfully installed duckdb-0.4.0
Name: duckdb
Version: 0.4.0
Summary: DuckDB embedded database
Home-page: https://www.duckdb.org
Author: None
Author-email: None
License: MIT
Location: /usr/local/lib/python3.7/dist-packages
Requires: numpy
Required-by:
Import the libraries:
import pandas as pd
import numpy as np
import duckdb
from matplotlib import pyplot as plt
# start an in-memory database
con = duckdb.connect(database=':memory:')
Transaction Data#
For the example reserving data, we use a simulated dataset from the SynthETIC R package, with further adjustments to it to make it resemble a real dataset.
DuckDB can read and query CSVs directly from local files - but with CSV files from the internet it is easier to read it with Python in pandas.
transactions = pd.read_csv(
"https://raw.githubusercontent.com/JackyP/SyntheticExports/main/synthetic_test_transaction_dataset.csv"
)
transactions
| claim_no | pmt_no | occurrence_period | occurrence_time | claim_size | notidel | setldel | payment_time | payment_period | payment_size | payment_inflated | payment_delay | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0.623835 | 785870.789628 | 0.065163 | 18.228022 | 4.197594 | 5 | 25104.778182 | 25631.935128 | 3.508595 |
| 1 | 1 | 2 | 1 | 0.623835 | 785870.789628 | 0.065163 | 18.228022 | 7.096012 | 8 | 26176.620067 | 27112.545886 | 2.898418 |
| 2 | 1 | 3 | 1 | 0.623835 | 785870.789628 | 0.065163 | 18.228022 | 11.157697 | 12 | 26333.186750 | 27828.701791 | 4.061685 |
| 3 | 1 | 4 | 1 | 0.623835 | 785870.789628 | 0.065163 | 18.228022 | 14.445762 | 15 | 26341.097381 | 28293.903794 | 3.288065 |
| 4 | 1 | 5 | 1 | 0.623835 | 785870.789628 | 0.065163 | 18.228022 | 18.452453 | 19 | 592456.913866 | 649127.994604 | 4.006691 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 18978 | 3624 | 2 | 40 | 39.767468 | 270737.291484 | 0.666458 | 2.920804 | 41.622132 | 42 | 6586.081338 | 8093.128975 | 0.670541 |
| 18979 | 3624 | 3 | 40 | 39.767468 | 270737.291484 | 0.666458 | 2.920804 | 42.081820 | 43 | 9716.975065 | 11967.648057 | 0.459688 |
| 18980 | 3624 | 4 | 40 | 39.767468 | 270737.291484 | 0.666458 | 2.920804 | 42.407479 | 43 | 7770.338755 | 9585.568042 | 0.325659 |
| 18981 | 3624 | 5 | 40 | 39.767468 | 270737.291484 | 0.666458 | 2.920804 | 43.066655 | 44 | 203618.760893 | 252007.199917 | 0.659176 |
| 18982 | 3624 | 6 | 40 | 39.767468 | 270737.291484 | 0.666458 | 2.920804 | 43.354731 | 44 | 34908.748394 | 43266.205665 | 0.288075 |
18983 rows × 12 columns
This is a transactional dataset with payments. The dataset has times are represented as arbitrary time period units rather than dates, and some additional calculated fields are already available. However, for this exercise, we want to demonstrate how to create these columns in real world situations where the raw datasets are unlikely to include them. So the time periods will be converted to date formats with months from a start date of 2000-01-01 and some columns hidden to create a dataset that resembles real datasets in practice.
# Feel free to skim through this part.
import datetime
from dateutil.relativedelta import relativedelta
dummy_start_date = datetime.date(2000, 1, 1)
transactions['occurrence_date'] = transactions.apply(
lambda x: (dummy_start_date +
relativedelta(months = int(x['occurrence_time'])) +
relativedelta(days = int(x['occurrence_time'] % 1 * 28))
),
axis = 1
)
transactions['payment_date'] = transactions.apply(
lambda x: (dummy_start_date +
relativedelta(months = int(x['payment_time'])) +
relativedelta(days = int(x['payment_time'] % 1 * 28))
),
axis = 1
)
transactions2 = transactions.loc[
lambda df: df.payment_time <= 40,
["claim_no", "pmt_no", "occurrence_date", "payment_date", "payment_size"]
]
So we will register this pandas table in SQL and pretend we had a dataset in our data warehouse that looks like this:
# register the table in sql
con.register('transactions_view', transactions2)
transactions2
| claim_no | pmt_no | occurrence_date | payment_date | payment_size | |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 2000-01-18 | 2000-05-06 | 25104.778182 |
| 1 | 1 | 2 | 2000-01-18 | 2000-08-03 | 26176.620067 |
| 2 | 1 | 3 | 2000-01-18 | 2000-12-05 | 26333.186750 |
| 3 | 1 | 4 | 2000-01-18 | 2001-03-13 | 26341.097381 |
| 4 | 1 | 5 | 2000-01-18 | 2001-07-13 | 592456.913866 |
| ... | ... | ... | ... | ... | ... |
| 18522 | 3540 | 1 | 2003-03-22 | 2003-04-15 | 7408.273603 |
| 18523 | 3540 | 2 | 2003-03-22 | 2003-04-23 | 7557.339854 |
| 18539 | 3543 | 1 | 2003-04-04 | 2003-04-25 | 11149.853130 |
| 18691 | 3570 | 1 | 2003-04-07 | 2003-04-26 | 3354.405206 |
| 18802 | 3588 | 1 | 2003-04-09 | 2003-04-26 | 2018.080359 |
14951 rows × 5 columns
Using SQL#
Here is the SQL query. It creates accident, development and payment/calendar periods from the dataset, and sums up at that triangle level. Uncomment claim_no and pmt_no to get a more detailed view - or for testing that the logic works.
con.execute("""
CREATE OR REPLACE VIEW triangle AS
SELECT
--claim_no,
--pmt_no,
DATE_DIFF('month', DATE '2000-01-01', STRPTIME(occurrence_date, '%Y-%m-%d')) + 1 as occurrence_period,
DATE_DIFF('month', DATE '2000-01-01', STRPTIME(payment_date, '%Y-%m-%d')) + 1 as payment_period,
DATE_DIFF('month', DATE '2000-01-01', STRPTIME(payment_date, '%Y-%m-%d')) -
DATE_DIFF('month', DATE '2000-01-01', STRPTIME(occurrence_date, '%Y-%m-%d')) + 1 as development_period,
SUM(payment_size) as payments
FROM
transactions_view
GROUP BY
--claim_no,
--pmt_no,
occurrence_period,
development_period,
payment_period
ORDER BY
--claim_no,
--pmt_no,
occurrence_period,
development_period,
payment_period
;
SELECT * FROM triangle;
"""
)
triangle = con.fetchdf()
triangle
| occurrence_period | payment_period | development_period | payments | |
|---|---|---|---|---|
| 0 | 1 | 2 | 2 | 46985.029619 |
| 1 | 1 | 3 | 3 | 392545.850638 |
| 2 | 1 | 4 | 4 | 185946.113394 |
| 3 | 1 | 5 | 5 | 700630.302735 |
| 4 | 1 | 6 | 6 | 261024.509136 |
| ... | ... | ... | ... | ... |
| 765 | 37 | 40 | 4 | 338030.875016 |
| 766 | 38 | 39 | 2 | 97489.963585 |
| 767 | 38 | 40 | 3 | 259540.894156 |
| 768 | 39 | 40 | 2 | 69383.491649 |
| 769 | 40 | 40 | 1 | 16522.338695 |
770 rows × 4 columns
Whilst the above is perfect for further calculations or export, triangles are often displayed in the “wide” format as follows. Pivotting is easier in pandas in Python (or R with dplyr::pivot_wider), than in SQL.
triangle.pivot(index="occurrence_period", columns="development_period", values="payments")
| development_period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| occurrence_period | |||||||||||||||||||||
| 1 | NaN | 46985.029619 | 392545.850638 | 1.859461e+05 | 7.006303e+05 | 2.610245e+05 | 3.329688e+05 | 2.646413e+05 | 6.057430e+05 | 1.434176e+05 | ... | 1.771805e+06 | 507751.595236 | 1.267975e+06 | 205780.737653 | 6226.894042 | NaN | 5.087788e+05 | 55918.782513 | NaN | 412516.399423 |
| 2 | 64334.385165 | 103991.537490 | 134383.992047 | 2.940818e+05 | 4.868833e+05 | 2.805029e+06 | 3.835312e+05 | 1.475784e+05 | 2.536358e+05 | 5.385814e+05 | ... | 8.616884e+04 | 8745.529181 | 3.974022e+05 | 714117.521603 | 89465.857732 | 128332.630805 | 5.301655e+05 | 349790.454839 | 12587.59026 | 90955.620959 |
| 3 | 3142.606330 | 43202.971210 | 156562.667084 | 2.792880e+05 | 5.374176e+05 | 4.028233e+05 | 6.908980e+05 | 4.429766e+05 | 7.212855e+05 | 8.362954e+05 | ... | NaN | 20938.965519 | NaN | NaN | 19996.986384 | NaN | NaN | NaN | NaN | NaN |
| 4 | NaN | 61865.265714 | 57298.919248 | 1.859610e+05 | 1.862006e+05 | 1.453144e+05 | 2.696107e+05 | 4.480261e+05 | 1.742546e+05 | 9.715882e+05 | ... | 4.688630e+05 | NaN | 6.155031e+05 | 197934.940768 | NaN | NaN | 3.830643e+05 | NaN | NaN | NaN |
| 5 | 5346.166482 | 54954.008437 | 264498.220981 | 2.036823e+05 | 4.472988e+05 | 2.633055e+05 | 3.387926e+05 | 3.150558e+05 | 7.504150e+05 | 2.611304e+05 | ... | 1.103665e+05 | 587681.103745 | 2.201814e+04 | 87364.263674 | NaN | 322793.116875 | 1.043557e+06 | NaN | NaN | NaN |
| 6 | 4222.377626 | 117425.751392 | 537503.282266 | 4.137136e+05 | 3.769690e+05 | 6.769168e+05 | 1.084063e+06 | 8.276801e+05 | 8.531432e+05 | 2.054070e+05 | ... | 6.795053e+04 | NaN | 1.900894e+06 | NaN | 189803.137289 | 165066.293055 | NaN | NaN | NaN | NaN |
| 7 | NaN | 51733.238185 | 121187.914637 | 2.782337e+05 | 3.766345e+05 | 5.262455e+05 | 4.970687e+05 | 6.972138e+05 | 7.314588e+05 | 6.290212e+05 | ... | 1.041520e+04 | 40683.584878 | 4.737402e+05 | NaN | 874535.741565 | NaN | NaN | NaN | NaN | NaN |
| 8 | NaN | 29161.090791 | 182951.743887 | 3.381624e+05 | 2.823336e+05 | 3.432786e+05 | 1.183421e+06 | 9.014267e+05 | 1.167906e+06 | 4.107145e+05 | ... | NaN | 493829.570893 | 3.123278e+05 | 58747.903282 | NaN | NaN | NaN | NaN | NaN | NaN |
| 9 | NaN | 133157.263191 | 215744.746038 | 1.374049e+06 | 7.828536e+05 | 7.966235e+05 | 4.644824e+05 | 9.741834e+05 | 5.535232e+05 | 5.008409e+05 | ... | 1.230771e+04 | 117212.190268 | 3.179059e+05 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 10 | NaN | 79641.863426 | 575926.050990 | 1.356863e+06 | 6.072203e+05 | 4.012266e+05 | 1.216483e+06 | 1.395769e+06 | 4.876399e+05 | 2.889569e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 11 | NaN | 100416.983371 | 292038.198343 | 4.448307e+05 | 5.126842e+05 | 3.632974e+05 | 1.872042e+06 | 8.211516e+05 | 5.397643e+05 | 4.108131e+05 | ... | 1.069290e+05 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 12 | NaN | 71522.558157 | 458885.392198 | 1.747373e+05 | 2.250982e+05 | 4.301923e+05 | 3.891993e+05 | 1.278298e+06 | 2.775127e+05 | 2.709438e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 13 | NaN | 79064.667239 | 254608.617474 | 4.293419e+05 | 1.876411e+06 | 5.398142e+05 | 6.579055e+05 | 8.572567e+05 | 3.248639e+05 | 2.372064e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 14 | NaN | 96277.421753 | 497171.088993 | 1.677511e+05 | 5.025259e+05 | 3.275906e+05 | 5.593842e+05 | 4.950296e+05 | 6.022564e+05 | 7.874864e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 15 | NaN | 21066.291384 | 131006.302772 | 2.469400e+05 | 1.794551e+05 | 2.232539e+05 | 4.005883e+05 | 1.158106e+06 | 1.432307e+06 | 4.311331e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 16 | NaN | 40871.450031 | 181169.969846 | 5.136258e+05 | 9.165714e+05 | 2.441091e+05 | 6.139660e+05 | 8.670557e+05 | 1.456116e+06 | 9.063431e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 17 | 21559.053170 | 98325.244742 | 111475.307366 | 6.413985e+05 | 6.213374e+05 | 7.985672e+05 | 1.252059e+06 | 9.138599e+05 | 1.066295e+06 | 3.610327e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 18 | NaN | 51441.830587 | 135464.967542 | 2.466380e+05 | 3.549195e+05 | 7.319261e+05 | 4.614343e+05 | 3.535514e+05 | 5.865144e+05 | 1.090865e+06 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 19 | NaN | 70653.792105 | 453457.316593 | 4.380374e+05 | 1.137775e+06 | 1.579018e+06 | 9.959784e+05 | 8.986285e+05 | 1.351723e+06 | 1.012969e+06 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 20 | NaN | 143003.416713 | 780501.376194 | 3.219736e+05 | 1.125306e+06 | 3.863964e+05 | 3.987071e+05 | 7.493505e+05 | 5.173210e+05 | 2.957905e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 21 | 440.166014 | 96436.510110 | 932830.920427 | 6.675994e+05 | 8.898485e+05 | 5.927916e+05 | 1.256132e+06 | 1.541598e+06 | 2.055776e+06 | 4.470712e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 22 | 5071.193962 | 114720.424477 | 407660.107716 | 4.120153e+05 | 3.215467e+05 | 4.644149e+05 | 1.129388e+06 | 7.422531e+05 | 2.230668e+06 | 1.509081e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 23 | NaN | 67368.580343 | 296994.656315 | 1.742078e+05 | 6.093717e+05 | 6.336027e+05 | 4.269155e+05 | 1.150700e+06 | 3.514760e+05 | 3.263753e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 24 | 2538.223611 | 60928.691028 | 474989.573924 | 2.655743e+05 | 3.890088e+05 | 7.493399e+05 | 1.231399e+06 | 6.559668e+05 | 6.981326e+05 | 3.937930e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 25 | 1179.531504 | 17397.734757 | 125719.238936 | 4.522247e+05 | 5.405587e+05 | 6.677909e+05 | 1.147964e+06 | 1.547991e+06 | 7.713320e+05 | 5.950225e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 26 | 18834.212213 | 54467.867400 | 301098.228443 | 1.205226e+06 | 6.651762e+05 | 1.773508e+06 | 2.409755e+05 | 3.835268e+05 | 1.634412e+06 | 4.614016e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 27 | NaN | 16208.391804 | 129023.820713 | 3.686506e+05 | 5.212379e+05 | 2.942529e+05 | 4.663017e+05 | 5.628172e+05 | 6.043287e+05 | 6.298926e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 28 | 15268.662911 | 394082.054498 | 221508.422890 | 2.374703e+05 | 2.292117e+05 | 4.800493e+05 | 8.586132e+05 | 4.008364e+05 | 1.122428e+06 | 3.405180e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 29 | 3088.130242 | 11868.998623 | 171285.569611 | 6.625948e+05 | 5.220645e+05 | 4.140340e+05 | 6.895261e+05 | 1.054986e+06 | 9.524665e+05 | 8.048602e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 30 | 5760.506354 | 154821.974483 | 655525.150619 | 4.317146e+05 | 1.124190e+06 | 2.260838e+05 | 6.135078e+05 | 4.430098e+05 | 1.993302e+05 | 2.101516e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 31 | 4495.370500 | 39937.684328 | 156494.223044 | 1.601225e+05 | 4.273681e+05 | 3.515268e+05 | 4.448231e+05 | 2.566694e+05 | 7.195764e+05 | 4.164395e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 32 | 9929.179761 | 74453.718579 | 371373.646586 | 1.127049e+06 | 8.716352e+05 | 7.048680e+05 | 4.415583e+05 | 9.356616e+05 | 5.691857e+05 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 33 | NaN | 20348.062312 | 170218.459706 | 3.565538e+05 | 1.227990e+06 | 4.104408e+05 | 5.005702e+05 | 9.153730e+05 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 34 | NaN | 60272.602312 | 244223.415605 | 6.362106e+05 | 7.611882e+05 | 4.975266e+05 | 1.682282e+06 | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 35 | NaN | 29157.569363 | 140597.374295 | 2.988598e+05 | 9.378148e+05 | 9.179868e+05 | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 36 | 1740.439458 | 71028.928995 | 159736.350719 | 4.944280e+05 | 5.790932e+05 | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 37 | 2417.098113 | 60756.081859 | 219417.111202 | 3.380309e+05 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 38 | NaN | 97489.963585 | 259540.894156 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 39 | NaN | 69383.491649 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 40 | 16522.338695 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
40 rows × 39 columns
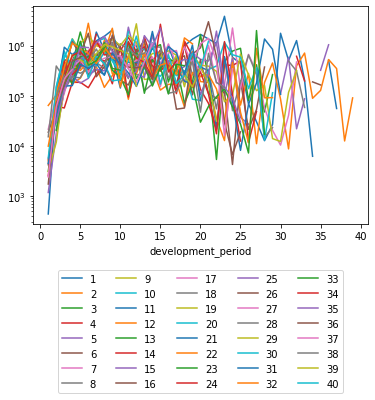
This can also be plotted easily with pandas.
(triangle
.pivot(index="development_period", columns="occurrence_period", values="payments")
.plot(logy=True)
)
plt.legend(loc="lower center", bbox_to_anchor=(0.5, -0.8), ncol=5)
<matplotlib.legend.Legend at 0x7f8126cd2d50>
Guaranteeing all cells#
With the above dataset, records will be missing if they do not have any claims transactions. This can be problematic if the models or calculations later on in the process flow rely on the dataset having every single accident/development period combination. To include these zero cells is not too difficult to implement in SQL.
The original dataset will be joined to a dummy dataset with the full range of accident/occurence and development periods.
# Dummy table of periods
range_occurrence = pd.DataFrame.from_dict({"occurrence_period": range(1, 40 + 1)})
range_development = pd.DataFrame.from_dict({"development_period": range(1, 40 + 1)})
range_occurrence
| occurrence_period | |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
| 6 | 7 |
| 7 | 8 |
| 8 | 9 |
| 9 | 10 |
| 10 | 11 |
| 11 | 12 |
| 12 | 13 |
| 13 | 14 |
| 14 | 15 |
| 15 | 16 |
| 16 | 17 |
| 17 | 18 |
| 18 | 19 |
| 19 | 20 |
| 20 | 21 |
| 21 | 22 |
| 22 | 23 |
| 23 | 24 |
| 24 | 25 |
| 25 | 26 |
| 26 | 27 |
| 27 | 28 |
| 28 | 29 |
| 29 | 30 |
| 30 | 31 |
| 31 | 32 |
| 32 | 33 |
| 33 | 34 |
| 34 | 35 |
| 35 | 36 |
| 36 | 37 |
| 37 | 38 |
| 38 | 39 |
| 39 | 40 |
con.register('range_occurrence_view', range_occurrence)
con.register('range_development_view', range_development)
<duckdb.DuckDBPyConnection at 0x7f813d8930b0>
The join logic can be constructed as follows. First full_tri is defined which has every combination of occurence and development period, then the original dataset is left joined onto it.
con.execute("""
CREATE OR REPLACE VIEW triangle_fill AS
WITH full_tri as (
SELECT
o.occurrence_period,
d.development_period,
d.development_period + o.occurrence_period - 1 as payment_period
FROM
range_occurrence_view as o,
range_development_view as d
)
SELECT
full_tri.*,
COALESCE(triangle.payments, 0) as payments
FROM
full_tri
LEFT JOIN
triangle
ON
full_tri.occurrence_period = triangle.occurrence_period
AND full_tri.development_period = triangle.development_period
AND full_tri.payment_period = triangle.payment_period
WHERE
full_tri.payment_period <= 40
-- if triangle is cut off at particular calendar period
;
SELECT * FROM triangle_fill;
"""
)
triangle_fill = con.fetchdf()
triangle_fill
| occurrence_period | development_period | payment_period | payments | |
|---|---|---|---|---|
| 0 | 1 | 2 | 2 | 46985.029619 |
| 1 | 1 | 3 | 3 | 392545.850638 |
| 2 | 1 | 4 | 4 | 185946.113394 |
| 3 | 1 | 5 | 5 | 700630.302735 |
| 4 | 1 | 6 | 6 | 261024.509136 |
| ... | ... | ... | ... | ... |
| 815 | 33 | 1 | 33 | 0.000000 |
| 816 | 34 | 1 | 34 | 0.000000 |
| 817 | 35 | 1 | 35 | 0.000000 |
| 818 | 38 | 1 | 38 | 0.000000 |
| 819 | 39 | 1 | 39 | 0.000000 |
820 rows × 4 columns
Again, here is the triangle. You can see the accident/development cells with no payments are now zero instead of null.
triangle_fill.pivot(index="occurrence_period", columns="development_period", values="payments")
| development_period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| occurrence_period | |||||||||||||||||||||
| 1 | 0.000000 | 46985.029619 | 392545.850638 | 1.859461e+05 | 7.006303e+05 | 2.610245e+05 | 3.329688e+05 | 2.646413e+05 | 6.057430e+05 | 1.434176e+05 | ... | 507751.595236 | 1.267975e+06 | 205780.737653 | 6226.894042 | 0.000000 | 5.087788e+05 | 55918.782513 | 0.00000 | 412516.399423 | 0.0 |
| 2 | 64334.385165 | 103991.537490 | 134383.992047 | 2.940818e+05 | 4.868833e+05 | 2.805029e+06 | 3.835312e+05 | 1.475784e+05 | 2.536358e+05 | 5.385814e+05 | ... | 8745.529181 | 3.974022e+05 | 714117.521603 | 89465.857732 | 128332.630805 | 5.301655e+05 | 349790.454839 | 12587.59026 | 90955.620959 | NaN |
| 3 | 3142.606330 | 43202.971210 | 156562.667084 | 2.792880e+05 | 5.374176e+05 | 4.028233e+05 | 6.908980e+05 | 4.429766e+05 | 7.212855e+05 | 8.362954e+05 | ... | 20938.965519 | 0.000000e+00 | 0.000000 | 19996.986384 | 0.000000 | 0.000000e+00 | 0.000000 | 0.00000 | NaN | NaN |
| 4 | 0.000000 | 61865.265714 | 57298.919248 | 1.859610e+05 | 1.862006e+05 | 1.453144e+05 | 2.696107e+05 | 4.480261e+05 | 1.742546e+05 | 9.715882e+05 | ... | 0.000000 | 6.155031e+05 | 197934.940768 | 0.000000 | 0.000000 | 3.830643e+05 | 0.000000 | NaN | NaN | NaN |
| 5 | 5346.166482 | 54954.008437 | 264498.220981 | 2.036823e+05 | 4.472988e+05 | 2.633055e+05 | 3.387926e+05 | 3.150558e+05 | 7.504150e+05 | 2.611304e+05 | ... | 587681.103745 | 2.201814e+04 | 87364.263674 | 0.000000 | 322793.116875 | 1.043557e+06 | NaN | NaN | NaN | NaN |
| 6 | 4222.377626 | 117425.751392 | 537503.282266 | 4.137136e+05 | 3.769690e+05 | 6.769168e+05 | 1.084063e+06 | 8.276801e+05 | 8.531432e+05 | 2.054070e+05 | ... | 0.000000 | 1.900894e+06 | 0.000000 | 189803.137289 | 165066.293055 | NaN | NaN | NaN | NaN | NaN |
| 7 | 0.000000 | 51733.238185 | 121187.914637 | 2.782337e+05 | 3.766345e+05 | 5.262455e+05 | 4.970687e+05 | 6.972138e+05 | 7.314588e+05 | 6.290212e+05 | ... | 40683.584878 | 4.737402e+05 | 0.000000 | 874535.741565 | NaN | NaN | NaN | NaN | NaN | NaN |
| 8 | 0.000000 | 29161.090791 | 182951.743887 | 3.381624e+05 | 2.823336e+05 | 3.432786e+05 | 1.183421e+06 | 9.014267e+05 | 1.167906e+06 | 4.107145e+05 | ... | 493829.570893 | 3.123278e+05 | 58747.903282 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 9 | 0.000000 | 133157.263191 | 215744.746038 | 1.374049e+06 | 7.828536e+05 | 7.966235e+05 | 4.644824e+05 | 9.741834e+05 | 5.535232e+05 | 5.008409e+05 | ... | 117212.190268 | 3.179059e+05 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 10 | 0.000000 | 79641.863426 | 575926.050990 | 1.356863e+06 | 6.072203e+05 | 4.012266e+05 | 1.216483e+06 | 1.395769e+06 | 4.876399e+05 | 2.889569e+05 | ... | 0.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 11 | 0.000000 | 100416.983371 | 292038.198343 | 4.448307e+05 | 5.126842e+05 | 3.632974e+05 | 1.872042e+06 | 8.211516e+05 | 5.397643e+05 | 4.108131e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 12 | 0.000000 | 71522.558157 | 458885.392198 | 1.747373e+05 | 2.250982e+05 | 4.301923e+05 | 3.891993e+05 | 1.278298e+06 | 2.775127e+05 | 2.709438e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 13 | 0.000000 | 79064.667239 | 254608.617474 | 4.293419e+05 | 1.876411e+06 | 5.398142e+05 | 6.579055e+05 | 8.572567e+05 | 3.248639e+05 | 2.372064e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 14 | 0.000000 | 96277.421753 | 497171.088993 | 1.677511e+05 | 5.025259e+05 | 3.275906e+05 | 5.593842e+05 | 4.950296e+05 | 6.022564e+05 | 7.874864e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 15 | 0.000000 | 21066.291384 | 131006.302772 | 2.469400e+05 | 1.794551e+05 | 2.232539e+05 | 4.005883e+05 | 1.158106e+06 | 1.432307e+06 | 4.311331e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 16 | 0.000000 | 40871.450031 | 181169.969846 | 5.136258e+05 | 9.165714e+05 | 2.441091e+05 | 6.139660e+05 | 8.670557e+05 | 1.456116e+06 | 9.063431e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 17 | 21559.053170 | 98325.244742 | 111475.307366 | 6.413985e+05 | 6.213374e+05 | 7.985672e+05 | 1.252059e+06 | 9.138599e+05 | 1.066295e+06 | 3.610327e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 18 | 0.000000 | 51441.830587 | 135464.967542 | 2.466380e+05 | 3.549195e+05 | 7.319261e+05 | 4.614343e+05 | 3.535514e+05 | 5.865144e+05 | 1.090865e+06 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 19 | 0.000000 | 70653.792105 | 453457.316593 | 4.380374e+05 | 1.137775e+06 | 1.579018e+06 | 9.959784e+05 | 8.986285e+05 | 1.351723e+06 | 1.012969e+06 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 20 | 0.000000 | 143003.416713 | 780501.376194 | 3.219736e+05 | 1.125306e+06 | 3.863964e+05 | 3.987071e+05 | 7.493505e+05 | 5.173210e+05 | 2.957905e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 21 | 440.166014 | 96436.510110 | 932830.920427 | 6.675994e+05 | 8.898485e+05 | 5.927916e+05 | 1.256132e+06 | 1.541598e+06 | 2.055776e+06 | 4.470712e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 22 | 5071.193962 | 114720.424477 | 407660.107716 | 4.120153e+05 | 3.215467e+05 | 4.644149e+05 | 1.129388e+06 | 7.422531e+05 | 2.230668e+06 | 1.509081e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 23 | 0.000000 | 67368.580343 | 296994.656315 | 1.742078e+05 | 6.093717e+05 | 6.336027e+05 | 4.269155e+05 | 1.150700e+06 | 3.514760e+05 | 3.263753e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 24 | 2538.223611 | 60928.691028 | 474989.573924 | 2.655743e+05 | 3.890088e+05 | 7.493399e+05 | 1.231399e+06 | 6.559668e+05 | 6.981326e+05 | 3.937930e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 25 | 1179.531504 | 17397.734757 | 125719.238936 | 4.522247e+05 | 5.405587e+05 | 6.677909e+05 | 1.147964e+06 | 1.547991e+06 | 7.713320e+05 | 5.950225e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 26 | 18834.212213 | 54467.867400 | 301098.228443 | 1.205226e+06 | 6.651762e+05 | 1.773508e+06 | 2.409755e+05 | 3.835268e+05 | 1.634412e+06 | 4.614016e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 27 | 0.000000 | 16208.391804 | 129023.820713 | 3.686506e+05 | 5.212379e+05 | 2.942529e+05 | 4.663017e+05 | 5.628172e+05 | 6.043287e+05 | 6.298926e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 28 | 15268.662911 | 394082.054498 | 221508.422890 | 2.374703e+05 | 2.292117e+05 | 4.800493e+05 | 8.586132e+05 | 4.008364e+05 | 1.122428e+06 | 3.405180e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 29 | 3088.130242 | 11868.998623 | 171285.569611 | 6.625948e+05 | 5.220645e+05 | 4.140340e+05 | 6.895261e+05 | 1.054986e+06 | 9.524665e+05 | 8.048602e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 30 | 5760.506354 | 154821.974483 | 655525.150619 | 4.317146e+05 | 1.124190e+06 | 2.260838e+05 | 6.135078e+05 | 4.430098e+05 | 1.993302e+05 | 2.101516e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 31 | 4495.370500 | 39937.684328 | 156494.223044 | 1.601225e+05 | 4.273681e+05 | 3.515268e+05 | 4.448231e+05 | 2.566694e+05 | 7.195764e+05 | 4.164395e+05 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 32 | 9929.179761 | 74453.718579 | 371373.646586 | 1.127049e+06 | 8.716352e+05 | 7.048680e+05 | 4.415583e+05 | 9.356616e+05 | 5.691857e+05 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 33 | 0.000000 | 20348.062312 | 170218.459706 | 3.565538e+05 | 1.227990e+06 | 4.104408e+05 | 5.005702e+05 | 9.153730e+05 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 34 | 0.000000 | 60272.602312 | 244223.415605 | 6.362106e+05 | 7.611882e+05 | 4.975266e+05 | 1.682282e+06 | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 35 | 0.000000 | 29157.569363 | 140597.374295 | 2.988598e+05 | 9.378148e+05 | 9.179868e+05 | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 36 | 1740.439458 | 71028.928995 | 159736.350719 | 4.944280e+05 | 5.790932e+05 | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 37 | 2417.098113 | 60756.081859 | 219417.111202 | 3.380309e+05 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 38 | 0.000000 | 97489.963585 | 259540.894156 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 39 | 0.000000 | 69383.491649 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 40 | 16522.338695 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
40 rows × 40 columns
Claims Ultimate Projections#
As demonstrated, it is fairly straightforward to transform claims data into the right format in SQL and create summaries for claims triangle projections.
Where to from here for claims ultimates? For further analysis in Excel, in Python (similar tools exist in R), pandas can export to xlsx format with to_excel, or xlwings can directly control Excel for additional VBA macro-style automation.
Triangle methods can also be applied directly within Python without exporting to Excel or another tool. Consider for example, chainladder, a project led out of casact which provides a number of claims development models. Or, alternatively we can do further calculations using pandas.
# Define a dataframe from the generated triangle
df_triangle_sort = triangle_fill.sort_values(['occurrence_period', 'development_period', 'payment_period'],
ascending=[True, True, True]).reset_index(drop=True)
# Add a column for cumulative payment
df_triangle_sort["payments_cumulative"] = \
df_triangle_sort.groupby(['occurrence_period'])['payments'] \
.cumsum(axis = 0)
#df_triangle_sort.head()
# Probably don't need this step but prints the triangle with cumulative payments
# Useful for at least some life companies who manually do this in Excel
IBNR_triangle_cumulative = \
df_triangle_sort.pivot(index = "occurrence_period", columns = "development_period",
values = "payments_cumulative").fillna(0)
#IBNR_triangle_cumulative
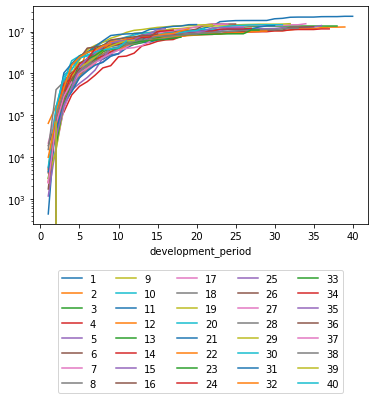
# Inspect claims development by occurrence period
(df_triangle_sort
.pivot(index = "development_period", columns = "occurrence_period", values = "payments_cumulative")
.plot(logy=True)
)
plt.legend(loc="lower center", bbox_to_anchor=(0.5, -0.8), ncol=5)
<matplotlib.legend.Legend at 0x7f81266db350>
(df_triangle_sort
.pivot(index = "development_period", columns = "occurrence_period", values = "payments_cumulative")
.plot(logy=True)
)
plt.legend(loc="lower center", bbox_to_anchor=(0.5, -0.8), ncol=5)
<matplotlib.legend.Legend at 0x7f8126a4fa10>

### 40 is the (hard-coded) cut-off as set out previously
### Get the diagonals in the cumulative IBNR triangle, which represents cumulative payments for a particular
### occurrence period
triangle_diagonal_interim = df_triangle_sort['payments_cumulative'][df_triangle_sort['payment_period'] == 40] \
.reset_index(drop = True)
triangle_diagonal_interim = pd.DataFrame(triangle_diagonal_interim).rename(columns = {'payments_cumulative': 'diagonal'})
triangle_diagonal = triangle_diagonal_interim.iloc[::-1].reset_index(drop = True)
### Sum cumulative payments by development period - to be used to calculate CDFs later
development_period_sum_interim = df_triangle_sort.groupby(by = 'development_period').sum()
development_period_sum = development_period_sum_interim['payments_cumulative'].reset_index(drop = True)
development_period_sum = pd.DataFrame(development_period_sum).rename(columns = {'payments_cumulative': 'dev_period_sum'})
# Merge two dataframes
df_cdf_interim = pd.concat([triangle_diagonal, development_period_sum], axis = 1)
#df_cdf_interim.head()
## dev_period_sum_alt column is to ensure the claims for two consecutive periods have the same number
## of levels/elements (and division of these two claims columns give the CDF)
df_cdf_interim['dev_period_sum_alt'] = df_cdf_interim['dev_period_sum'] - df_cdf_interim['diagonal']
### Show numbers in ,000 so they fit in the print
df_cdf = df_cdf_interim / 1000
df_cdf.head()
| diagonal | dev_period_sum | dev_period_sum_alt | |
|---|---|---|---|
| 0 | 16.522339 | 185.889642 | 169.367303 |
| 1 | 69.383492 | 3175.258309 | 3105.874818 |
| 2 | 357.030858 | 14478.493908 | 14121.463050 |
| 3 | 620.621166 | 30945.250969 | 30324.629803 |
| 4 | 1306.026932 | 53178.458717 | 51872.431785 |
### Calculate CDFs and IBNR
df_cdf['dev_period_sum_shift'] = df_cdf['dev_period_sum'].shift(-1)
df_cdf['CDF'] = df_cdf['dev_period_sum_shift'] / df_cdf['dev_period_sum_alt']
df_cdf['IBNR'] = df_cdf['diagonal'] * df_cdf['CDF'] - df_cdf['diagonal']
df_cdf
| diagonal | dev_period_sum | dev_period_sum_alt | dev_period_sum_shift | CDF | IBNR | |
|---|---|---|---|---|---|---|
| 0 | 16.522339 | 185.889642 | 169.367303 | 3175.258309 | 18.747764 | 2.932346e+02 |
| 1 | 69.383492 | 3175.258309 | 3105.874818 | 14478.493908 | 4.661648 | 2.540579e+02 |
| 2 | 357.030858 | 14478.493908 | 14121.463050 | 30945.250969 | 2.191363 | 4.253533e+02 |
| 3 | 620.621166 | 30945.250969 | 30324.629803 | 53178.458717 | 1.753639 | 4.677244e+02 |
| 4 | 1306.026932 | 53178.458717 | 51872.431785 | 73296.602164 | 1.413017 | 5.394107e+02 |
| 5 | 2324.416373 | 73296.602164 | 70972.185791 | 96164.725611 | 1.354964 | 8.250831e+02 |
| 6 | 3881.703186 | 96164.725611 | 92283.022426 | 117681.250228 | 1.275221 | 1.068326e+03 |
| 7 | 3601.493888 | 117681.250228 | 114079.756340 | 140442.547454 | 1.231091 | 8.322724e+02 |
| 8 | 5105.714463 | 140442.547454 | 135336.832990 | 150703.802943 | 1.113546 | 5.797340e+02 |
| 9 | 2977.453115 | 150703.802943 | 147726.349828 | 170044.443445 | 1.151077 | 4.498255e+02 |
| 10 | 5956.335308 | 170044.443445 | 164088.108137 | 183005.577081 | 1.115288 | 6.866969e+02 |
| 11 | 6137.892385 | 183005.577081 | 176867.684696 | 194064.476765 | 1.097230 | 5.967854e+02 |
| 12 | 6525.720481 | 194064.476765 | 187538.756284 | 204287.060802 | 1.089306 | 5.827849e+02 |
| 13 | 5723.672400 | 204287.060802 | 198563.388401 | 215573.572100 | 1.085666 | 4.903256e+02 |
| 14 | 8773.672508 | 215573.572100 | 206799.899593 | 218923.772211 | 1.058626 | 5.143662e+02 |
| 15 | 11645.898736 | 218923.772211 | 207277.873475 | 216004.148686 | 1.042099 | 4.902854e+02 |
| 16 | 10863.724549 | 216004.148686 | 205140.424136 | 216470.769285 | 1.055232 | 6.000268e+02 |
| 17 | 7327.527797 | 216470.769285 | 209143.241487 | 220337.077242 | 1.053522 | 3.921864e+02 |
| 18 | 11501.671667 | 220337.077242 | 208835.405575 | 218513.283493 | 1.046342 | 5.330120e+02 |
| 19 | 14660.109415 | 218513.283493 | 203853.174078 | 215920.240672 | 1.059195 | 8.678036e+02 |
| 20 | 11806.728149 | 215920.240672 | 204113.512524 | 210996.759170 | 1.033723 | 3.981541e+02 |
| 21 | 14524.793890 | 210996.759170 | 196471.965280 | 205781.727071 | 1.047385 | 6.882528e+02 |
| 22 | 9737.849633 | 205781.727071 | 196043.877438 | 203195.894048 | 1.036482 | 3.552534e+02 |
| 23 | 15208.011233 | 203195.894048 | 187987.882815 | 191860.497821 | 1.020600 | 3.132903e+02 |
| 24 | 15112.028525 | 191860.497821 | 176748.469296 | 179054.011348 | 1.013044 | 1.971243e+02 |
| 25 | 12505.126742 | 179054.011348 | 166548.884606 | 171642.608408 | 1.030584 | 3.824562e+02 |
| 26 | 11949.795402 | 171642.608408 | 159692.813006 | 162303.166569 | 1.016346 | 1.953325e+02 |
| 27 | 10869.297362 | 162303.166569 | 151433.869207 | 153292.830032 | 1.012276 | 1.334285e+02 |
| 28 | 10278.079946 | 153292.830032 | 143014.750086 | 145649.556309 | 1.018423 | 1.893563e+02 |
| 29 | 13793.567522 | 145649.556309 | 131855.988788 | 133632.831327 | 1.013476 | 1.858770e+02 |
| 30 | 14555.869668 | 133632.831327 | 119076.961659 | 124384.728333 | 1.044574 | 6.488170e+02 |
| 31 | 15414.760743 | 124384.728333 | 108969.967590 | 110233.912957 | 1.011599 | 1.787962e+02 |
| 32 | 12014.925334 | 110233.912957 | 98218.987623 | 99399.016240 | 1.012014 | 1.443505e+02 |
| 33 | 15374.786418 | 99399.016240 | 84024.229822 | 84640.421863 | 1.007334 | 1.127511e+02 |
| 34 | 13050.851980 | 84640.421863 | 71589.569883 | 74055.135038 | 1.034440 | 4.494751e+02 |
| 35 | 13885.641167 | 74055.135038 | 60169.493871 | 60575.203108 | 1.006743 | 9.362773e+01 |
| 36 | 11566.354056 | 60575.203108 | 49008.849052 | 49021.436642 | 1.000257 | 2.970740e+00 |
| 37 | 13545.590250 | 49021.436642 | 35475.846392 | 35979.318412 | 1.014192 | 1.922386e+02 |
| 38 | 12844.804666 | 35979.318412 | 23134.513746 | 23134.513746 | 1.000000 | -1.818989e-12 |
| 39 | 23134.513746 | 23134.513746 | 0.000000 | NaN | NaN | NaN |
pd.DataFrame(IBNR_triangle_cumulative/1000).round(0)
| development_period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| occurrence_period | ||||||||||||||||||||||||||||||||||||||||
| 1 | 0.0 | 47.0 | 440.0 | 625.0 | 1326.0 | 1587.0 | 1920.0 | 2185.0 | 2790.0 | 2934.0 | 4022.0 | 5022.0 | 5439.0 | 5603.0 | 6282.0 | 6701.0 | 6858.0 | 7857.0 | 9210.0 | 10895.0 | 12255.0 | 13365.0 | 17229.0 | 17816.0 | 18258.0 | 18328.0 | 18358.0 | 18371.0 | 18398.0 | 20170.0 | 20677.0 | 21945.0 | 22151.0 | 22157.0 | 22157.0 | 22666.0 | 22722.0 | 22722.0 | 23135.0 | 23135.0 |
| 2 | 64.0 | 168.0 | 303.0 | 597.0 | 1084.0 | 3889.0 | 4272.0 | 4420.0 | 4673.0 | 5212.0 | 5298.0 | 5855.0 | 6566.0 | 6923.0 | 7054.0 | 7223.0 | 7392.0 | 7667.0 | 8434.0 | 8627.0 | 8812.0 | 8848.0 | 8861.0 | 9443.0 | 9509.0 | 9789.0 | 9800.0 | 9984.0 | 10437.0 | 10523.0 | 10532.0 | 10929.0 | 11644.0 | 11733.0 | 11861.0 | 12391.0 | 12741.0 | 12754.0 | 12845.0 | 0.0 |
| 3 | 3.0 | 46.0 | 203.0 | 482.0 | 1020.0 | 1422.0 | 2113.0 | 2556.0 | 3278.0 | 4114.0 | 4489.0 | 4942.0 | 5453.0 | 6346.0 | 7395.0 | 7584.0 | 8185.0 | 8461.0 | 8647.0 | 10312.0 | 10539.0 | 10544.0 | 11024.0 | 11805.0 | 12693.0 | 12774.0 | 13191.0 | 13239.0 | 13505.0 | 13505.0 | 13526.0 | 13526.0 | 13526.0 | 13546.0 | 13546.0 | 13546.0 | 13546.0 | 13546.0 | 0.0 | 0.0 |
| 4 | 0.0 | 62.0 | 119.0 | 305.0 | 491.0 | 637.0 | 906.0 | 1354.0 | 1529.0 | 2500.0 | 2595.0 | 3045.0 | 4530.0 | 5027.0 | 5848.0 | 6313.0 | 6433.0 | 7674.0 | 8298.0 | 8433.0 | 8504.0 | 8525.0 | 8941.0 | 9345.0 | 9840.0 | 9852.0 | 9901.0 | 9901.0 | 9901.0 | 10370.0 | 10370.0 | 10985.0 | 11183.0 | 11183.0 | 11183.0 | 11566.0 | 11566.0 | 0.0 | 0.0 | 0.0 |
| 5 | 5.0 | 60.0 | 325.0 | 528.0 | 976.0 | 1239.0 | 1578.0 | 1893.0 | 2643.0 | 2904.0 | 5246.0 | 5791.0 | 6055.0 | 6424.0 | 6750.0 | 7129.0 | 7435.0 | 7819.0 | 8532.0 | 9068.0 | 9562.0 | 10706.0 | 10807.0 | 11375.0 | 11412.0 | 11440.0 | 11440.0 | 11712.0 | 11712.0 | 11822.0 | 12410.0 | 12432.0 | 12519.0 | 12519.0 | 12842.0 | 13886.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 6 | 4.0 | 122.0 | 659.0 | 1073.0 | 1450.0 | 2127.0 | 3211.0 | 4038.0 | 4892.0 | 5097.0 | 5262.0 | 5681.0 | 6627.0 | 7112.0 | 7480.0 | 7969.0 | 8490.0 | 9119.0 | 9223.0 | 9750.0 | 9862.0 | 9951.0 | 10073.0 | 10077.0 | 10277.0 | 10298.0 | 10352.0 | 10727.0 | 10727.0 | 10795.0 | 10795.0 | 12696.0 | 12696.0 | 12886.0 | 13051.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 | 0.0 | 52.0 | 173.0 | 451.0 | 828.0 | 1354.0 | 1851.0 | 2548.0 | 3280.0 | 3909.0 | 4255.0 | 5469.0 | 5847.0 | 6446.0 | 6599.0 | 7312.0 | 8114.0 | 8301.0 | 8867.0 | 9161.0 | 10179.0 | 10363.0 | 10527.0 | 12782.0 | 12922.0 | 13594.0 | 13897.0 | 13955.0 | 13975.0 | 13986.0 | 14027.0 | 14500.0 | 14500.0 | 15375.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 | 0.0 | 29.0 | 212.0 | 550.0 | 833.0 | 1176.0 | 2359.0 | 3261.0 | 4429.0 | 4839.0 | 5060.0 | 5830.0 | 5956.0 | 6128.0 | 6926.0 | 7158.0 | 7474.0 | 8486.0 | 8750.0 | 8994.0 | 9313.0 | 9368.0 | 9951.0 | 10002.0 | 10190.0 | 10846.0 | 11112.0 | 11127.0 | 11150.0 | 11150.0 | 11644.0 | 11956.0 | 12015.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 | 0.0 | 133.0 | 349.0 | 1723.0 | 2506.0 | 3302.0 | 3767.0 | 4741.0 | 5295.0 | 5795.0 | 6357.0 | 9091.0 | 9303.0 | 9524.0 | 10177.0 | 10969.0 | 11617.0 | 11769.0 | 12434.0 | 12843.0 | 13234.0 | 13543.0 | 13620.0 | 13722.0 | 14403.0 | 14665.0 | 14792.0 | 14953.0 | 14967.0 | 14980.0 | 15097.0 | 15415.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 | 0.0 | 80.0 | 656.0 | 2012.0 | 2620.0 | 3021.0 | 4237.0 | 5633.0 | 6121.0 | 6410.0 | 7471.0 | 8232.0 | 9125.0 | 9402.0 | 9649.0 | 10036.0 | 10288.0 | 10606.0 | 10692.0 | 10773.0 | 11107.0 | 11502.0 | 12665.0 | 13327.0 | 13918.0 | 14057.0 | 14427.0 | 14441.0 | 14556.0 | 14556.0 | 14556.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 | 0.0 | 100.0 | 392.0 | 837.0 | 1350.0 | 1713.0 | 3585.0 | 4406.0 | 4946.0 | 5357.0 | 5825.0 | 6296.0 | 6671.0 | 7567.0 | 8109.0 | 9089.0 | 9449.0 | 9645.0 | 9816.0 | 10193.0 | 10511.0 | 10533.0 | 11141.0 | 11220.0 | 11228.0 | 11296.0 | 11477.0 | 12838.0 | 13687.0 | 13794.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12 | 0.0 | 72.0 | 530.0 | 705.0 | 930.0 | 1360.0 | 1750.0 | 3028.0 | 3305.0 | 3576.0 | 4700.0 | 5204.0 | 6328.0 | 6642.0 | 7046.0 | 7467.0 | 7656.0 | 7716.0 | 8008.0 | 8248.0 | 8516.0 | 8653.0 | 8683.0 | 9149.0 | 9196.0 | 9207.0 | 10094.0 | 10186.0 | 10278.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 | 0.0 | 79.0 | 334.0 | 763.0 | 2639.0 | 3179.0 | 3837.0 | 4694.0 | 5019.0 | 5256.0 | 5361.0 | 6215.0 | 6327.0 | 6855.0 | 7189.0 | 7780.0 | 8183.0 | 8255.0 | 8425.0 | 8455.0 | 8517.0 | 8613.0 | 8750.0 | 8810.0 | 8838.0 | 8845.0 | 10852.0 | 10869.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 14 | 0.0 | 96.0 | 593.0 | 761.0 | 1264.0 | 1591.0 | 2151.0 | 2646.0 | 3248.0 | 4035.0 | 5510.0 | 6270.0 | 7222.0 | 7618.0 | 7929.0 | 8424.0 | 8535.0 | 9656.0 | 9804.0 | 10104.0 | 10214.0 | 10231.0 | 11440.0 | 11546.0 | 11559.0 | 11559.0 | 11950.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 15 | 0.0 | 21.0 | 152.0 | 399.0 | 578.0 | 802.0 | 1202.0 | 2360.0 | 3793.0 | 4224.0 | 5363.0 | 5631.0 | 5866.0 | 7500.0 | 7935.0 | 8432.0 | 8876.0 | 9410.0 | 9902.0 | 10008.0 | 10280.0 | 12234.0 | 12383.0 | 12475.0 | 12505.0 | 12505.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 16 | 0.0 | 41.0 | 222.0 | 736.0 | 1652.0 | 1896.0 | 2510.0 | 3377.0 | 4833.0 | 5740.0 | 6286.0 | 7045.0 | 8313.0 | 8548.0 | 9286.0 | 9738.0 | 9793.0 | 9850.0 | 10534.0 | 11440.0 | 14453.0 | 15057.0 | 15086.0 | 15093.0 | 15112.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 17 | 22.0 | 120.0 | 231.0 | 873.0 | 1494.0 | 2293.0 | 3545.0 | 4459.0 | 5525.0 | 5886.0 | 6304.0 | 6815.0 | 7437.0 | 8538.0 | 8954.0 | 10040.0 | 10470.0 | 11418.0 | 11862.0 | 12955.0 | 14357.0 | 14847.0 | 14863.0 | 15208.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 18 | 0.0 | 51.0 | 187.0 | 434.0 | 788.0 | 1520.0 | 1982.0 | 2335.0 | 2922.0 | 4013.0 | 4852.0 | 5183.0 | 5790.0 | 6744.0 | 7683.0 | 7796.0 | 7918.0 | 8170.0 | 8652.0 | 8699.0 | 9406.0 | 9590.0 | 9738.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 19 | 0.0 | 71.0 | 524.0 | 962.0 | 2100.0 | 3679.0 | 4675.0 | 5574.0 | 6925.0 | 7938.0 | 9539.0 | 10685.0 | 11163.0 | 11861.0 | 12571.0 | 12899.0 | 13534.0 | 13790.0 | 13940.0 | 14312.0 | 14493.0 | 14525.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 20 | 0.0 | 143.0 | 924.0 | 1245.0 | 2371.0 | 2757.0 | 3156.0 | 3905.0 | 4423.0 | 4718.0 | 5204.0 | 6757.0 | 7100.0 | 8247.0 | 8418.0 | 9080.0 | 9255.0 | 9523.0 | 10225.0 | 10584.0 | 11807.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 21 | 0.0 | 97.0 | 1030.0 | 1697.0 | 2587.0 | 3180.0 | 4436.0 | 5978.0 | 8033.0 | 8481.0 | 8768.0 | 8922.0 | 9301.0 | 11224.0 | 11595.0 | 12560.0 | 13275.0 | 13541.0 | 14580.0 | 14660.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 22 | 5.0 | 120.0 | 527.0 | 939.0 | 1261.0 | 1725.0 | 2855.0 | 3597.0 | 5828.0 | 5979.0 | 6621.0 | 6893.0 | 7624.0 | 7844.0 | 8257.0 | 8712.0 | 8980.0 | 10412.0 | 11502.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 23 | 0.0 | 67.0 | 364.0 | 539.0 | 1148.0 | 1782.0 | 2208.0 | 3359.0 | 3711.0 | 4037.0 | 5257.0 | 5477.0 | 5867.0 | 6024.0 | 6393.0 | 6502.0 | 6930.0 | 7328.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 24 | 3.0 | 63.0 | 538.0 | 804.0 | 1193.0 | 1942.0 | 3174.0 | 3830.0 | 4528.0 | 4922.0 | 6122.0 | 6692.0 | 7158.0 | 7387.0 | 10066.0 | 10365.0 | 10864.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 25 | 1.0 | 19.0 | 144.0 | 597.0 | 1137.0 | 1805.0 | 2953.0 | 4501.0 | 5272.0 | 5867.0 | 6102.0 | 6407.0 | 7996.0 | 8950.0 | 11206.0 | 11646.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 26 | 19.0 | 73.0 | 374.0 | 1580.0 | 2245.0 | 4018.0 | 4259.0 | 4643.0 | 6277.0 | 6739.0 | 7109.0 | 7472.0 | 7866.0 | 8078.0 | 8774.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 27 | 0.0 | 16.0 | 145.0 | 514.0 | 1035.0 | 1329.0 | 1796.0 | 2358.0 | 2963.0 | 3593.0 | 3943.0 | 4129.0 | 4609.0 | 5724.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 28 | 15.0 | 409.0 | 631.0 | 868.0 | 1098.0 | 1578.0 | 2436.0 | 2837.0 | 3959.0 | 4300.0 | 5187.0 | 5818.0 | 6526.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 29 | 3.0 | 15.0 | 186.0 | 849.0 | 1371.0 | 1785.0 | 2474.0 | 3529.0 | 4482.0 | 5287.0 | 5980.0 | 6138.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 30 | 6.0 | 161.0 | 816.0 | 1248.0 | 2372.0 | 2598.0 | 3212.0 | 3655.0 | 3854.0 | 4064.0 | 5956.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 31 | 4.0 | 44.0 | 201.0 | 361.0 | 788.0 | 1140.0 | 1585.0 | 1841.0 | 2561.0 | 2977.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 32 | 10.0 | 84.0 | 456.0 | 1583.0 | 2454.0 | 3159.0 | 3601.0 | 4537.0 | 5106.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 33 | 0.0 | 20.0 | 191.0 | 547.0 | 1775.0 | 2186.0 | 2686.0 | 3601.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 34 | 0.0 | 60.0 | 304.0 | 941.0 | 1702.0 | 2199.0 | 3882.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 35 | 0.0 | 29.0 | 170.0 | 469.0 | 1406.0 | 2324.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 36 | 2.0 | 73.0 | 233.0 | 727.0 | 1306.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 37 | 2.0 | 63.0 | 283.0 | 621.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 38 | 0.0 | 97.0 | 357.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 39 | 0.0 | 69.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 40 | 17.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
